Physics:Virtual displacement
In analytical mechanics, a branch of applied mathematics and physics, a virtual displacement (or infinitesimal variation) [math]\displaystyle{ \delta \gamma }[/math] shows how the mechanical system's trajectory can hypothetically (hence the term virtual) deviate very slightly from the actual trajectory [math]\displaystyle{ \gamma }[/math] of the system without violating the system's constraints.[1][2][3]:263 For every time instant [math]\displaystyle{ t, }[/math] [math]\displaystyle{ \delta \gamma(t) }[/math] is a vector tangential to the configuration space at the point [math]\displaystyle{ \gamma(t). }[/math] The vectors [math]\displaystyle{ \delta \gamma(t) }[/math] show the directions in which [math]\displaystyle{ \gamma(t) }[/math] can "go" without breaking the constraints.
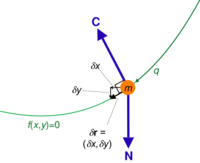
For example, the virtual displacements of the system consisting of a single particle on a two-dimensional surface fill up the entire tangent plane, assuming there are no additional constraints.
If, however, the constraints require that all the trajectories [math]\displaystyle{ \gamma }[/math] pass through the given point [math]\displaystyle{ \mathbf{q} }[/math] at the given time [math]\displaystyle{ \tau, }[/math] i.e. [math]\displaystyle{ \gamma(\tau) = \mathbf{q}, }[/math] then [math]\displaystyle{ \delta\gamma (\tau) = 0. }[/math]
Notations
Let [math]\displaystyle{ M }[/math] be the configuration space of the mechanical system, [math]\displaystyle{ t_0,t_1 \in \mathbb{R} }[/math] be time instants, [math]\displaystyle{ q_0,q_1 \in M, }[/math] [math]\displaystyle{ C^\infty[t_0, t_1] }[/math] consists of smooth functions on [math]\displaystyle{ [t_0, t_1] }[/math], and
[math]\displaystyle{ P(M) = \{\gamma \in C^\infty([t_0,t_1], M) \mid \gamma(t_0)=q_0,\ \gamma(t_1)=q_1\}. }[/math]
The constraints [math]\displaystyle{ \gamma(t_0)=q_0, }[/math] [math]\displaystyle{ \gamma(t_1)=q_1 }[/math] are here for illustration only. In practice, for each individual system, an individual set of constraints is required.
Definition
For each path [math]\displaystyle{ \gamma \in P(M) }[/math] and [math]\displaystyle{ \epsilon_0 \gt 0, }[/math] a variation of [math]\displaystyle{ \gamma }[/math] is a function [math]\displaystyle{ \Gamma : [t_0,t_1] \times [-\epsilon_0,\epsilon_0] \to M }[/math] such that, for every [math]\displaystyle{ \epsilon \in [-\epsilon_0,\epsilon_0], }[/math] [math]\displaystyle{ \Gamma(\cdot,\epsilon) \in P(M) }[/math] and [math]\displaystyle{ \Gamma(t,0) = \gamma(t). }[/math] The virtual displacement [math]\displaystyle{ \delta \gamma : [t_0,t_1] \to TM }[/math] [math]\displaystyle{ (TM }[/math] being the tangent bundle of [math]\displaystyle{ M) }[/math] corresponding to the variation [math]\displaystyle{ \Gamma }[/math] assigns[1] to every [math]\displaystyle{ t \in [t_0,t_1] }[/math] the tangent vector
[math]\displaystyle{ \delta \gamma(t) = \frac{d\Gamma(t,\epsilon)}{d\epsilon}\Biggl|_{\epsilon=0} \in T_{\gamma(t)}M. }[/math]
In terms of the tangent map,
[math]\displaystyle{ \delta \gamma(t) = \Gamma^t_*\left(\frac{d}{d\epsilon}\Biggl|_{\epsilon=0}\right). }[/math]
Here [math]\displaystyle{ \Gamma^t_*: T_0[-\epsilon,\epsilon] \to T_{\Gamma(t,0)}M = T_{\gamma(t)}M }[/math] is the tangent map of [math]\displaystyle{ \Gamma^t : [-\epsilon,\epsilon] \to M, }[/math] where [math]\displaystyle{ \Gamma^t(\epsilon) = \Gamma(t,\epsilon), }[/math] and [math]\displaystyle{ \textstyle \frac{d}{d\epsilon}\Bigl|_{\epsilon = 0} \in T_0[-\epsilon,\epsilon]. }[/math]
Properties
- Coordinate representation. If [math]\displaystyle{ \{q_i\}^n_{i=1} }[/math] are the coordinates in an arbitrary chart on [math]\displaystyle{ M }[/math] and [math]\displaystyle{ n = \mathop{\rm dim}M, }[/math] then
- [math]\displaystyle{ \delta \gamma(t) = \sum^n_{i=1} \frac{d[q_i(\Gamma(t,\epsilon))]}{d\epsilon}\Biggl|_{\epsilon=0} \cdot \frac{d}{dq_i}\Biggl|_{\gamma(t)}. }[/math]
- If, for some time instant [math]\displaystyle{ \tau }[/math] and every [math]\displaystyle{ \gamma \in P(M), }[/math] [math]\displaystyle{ \gamma(\tau)=\text{const}, }[/math] then, for every [math]\displaystyle{ \gamma \in P(M), }[/math] [math]\displaystyle{ \delta \gamma (\tau) = 0. }[/math]
- If [math]\displaystyle{ \textstyle \gamma,\frac{d\gamma}{dt} \in P(M), }[/math] then [math]\displaystyle{ \delta \frac{d\gamma}{dt} = \frac{d}{dt}\delta \gamma. }[/math]
Examples
Free particle in R3
A single particle freely moving in [math]\displaystyle{ \mathbb{R}^3 }[/math] has 3 degrees of freedom. The configuration space is [math]\displaystyle{ M=\mathbb{R}^3, }[/math] and [math]\displaystyle{ P(M)=C^\infty([t_0,t_1], M). }[/math] For every path [math]\displaystyle{ \gamma \in P(M) }[/math] and a variation [math]\displaystyle{ \Gamma(t,\epsilon) }[/math] of [math]\displaystyle{ \gamma, }[/math] there exists a unique [math]\displaystyle{ \sigma \in T_0\mathbb{R}^3 }[/math] such that [math]\displaystyle{ \Gamma(t,\epsilon) = \gamma(t) + \sigma(t)\epsilon + o(\epsilon), }[/math] as [math]\displaystyle{ \epsilon \to 0. }[/math] By the definition,
[math]\displaystyle{ \delta \gamma (t) = \left(\frac{d}{d\epsilon} \Bigl(\gamma(t) + \sigma(t)\epsilon + o(\epsilon)\Bigr)\right)\Biggl|_{\epsilon=0} }[/math]
which leads to
[math]\displaystyle{ \delta \gamma (t) = \sigma(t) \in T_{\gamma(t)} \mathbb{R}^3. }[/math]
Free particles on a surface
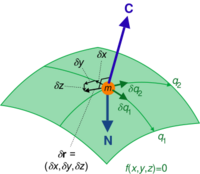
[math]\displaystyle{ N }[/math] particles moving freely on a two-dimensional surface [math]\displaystyle{ S \subset \mathbb{R}^3 }[/math] have [math]\displaystyle{ 2N }[/math] degree of freedom. The configuration space here is
[math]\displaystyle{ M= \{(\mathbf{r}_1, \ldots, \mathbf{r}_N)\in \mathbb{R}^{3\, N} \mid \mathbf{r}_i \in \mathbb{R}^3;\ \mathbf{r}_i \neq \mathbf{r}_j\ \text{if}\ i \neq j\}, }[/math]
where [math]\displaystyle{ \mathbf{r}_i \in \mathbb{R}^3 }[/math] is the radius vector of the [math]\displaystyle{ i^\text{th} }[/math] particle. It follows that
[math]\displaystyle{ T_{(\mathbf{r}_1, \ldots, \mathbf{r}_N)} M = T_{\mathbf{r}_1}S \oplus \ldots \oplus T_{\mathbf{r}_N}S, }[/math]
and every path [math]\displaystyle{ \gamma \in P(M) }[/math] may be described using the radius vectors [math]\displaystyle{ \mathbf{r}_i }[/math] of each individual particle, i.e.
[math]\displaystyle{ \gamma (t) = (\mathbf{r}_1(t),\ldots, \mathbf{r}_N(t)). }[/math]
This implies that, for every [math]\displaystyle{ \delta \gamma(t) \in T_{(\mathbf{r}_1(t), \ldots, \mathbf{r}_N(t))} M, }[/math]
[math]\displaystyle{ \delta \gamma(t) = \delta \mathbf{r}_1(t) \oplus \ldots \oplus \delta \mathbf{r}_N(t), }[/math]
where [math]\displaystyle{ \delta \mathbf{r}_i(t) \in T_{\mathbf{r}_i(t)} S. }[/math] Some authors express this as
[math]\displaystyle{ \delta \gamma = (\delta \mathbf{r}_1, \ldots , \delta \mathbf{r}_N). }[/math]
Rigid body rotating around fixed point
A rigid body rotating around a fixed point with no additional constraints has 3 degrees of freedom. The configuration space here is [math]\displaystyle{ M=SO(3), }[/math] the special orthogonal group of dimension 3 (otherwise known as 3D rotation group), and [math]\displaystyle{ P(M)=C^\infty([t_0,t_1], M). }[/math] We use the standard notation [math]\displaystyle{ \mathfrak{so}(3) }[/math] to refer to the three-dimensional linear space of all skew-symmetric three-dimensional matrices. The exponential map [math]\displaystyle{ \exp : \mathfrak{so}(3) \to SO(3) }[/math] guarantees the existence of [math]\displaystyle{ \epsilon_0 \gt 0 }[/math] such that, for every path [math]\displaystyle{ \gamma \in P(M), }[/math] its variation [math]\displaystyle{ \Gamma(t,\epsilon), }[/math] and [math]\displaystyle{ t \in [t_0,t_1], }[/math] there is a unique path [math]\displaystyle{ \Theta^t \in C^\infty([-\epsilon_0, \epsilon_0], \mathfrak{so}(3)) }[/math] such that [math]\displaystyle{ \Theta^t(0) = 0 }[/math] and, for every [math]\displaystyle{ \epsilon \in [-\epsilon_0,\epsilon_0], }[/math] [math]\displaystyle{ \Gamma(t,\epsilon) = \gamma(t)\exp(\Theta^t(\epsilon)). }[/math] By the definition,
[math]\displaystyle{ \delta \gamma (t) = \left(\frac{d}{d\epsilon} \Bigl(\gamma(t)\exp(\Theta^t(\epsilon))\Bigr)\right)\Biggl|_{\epsilon=0} = \gamma(t)\frac{d\Theta^t(\epsilon)}{d\epsilon}\Biggl|_{\epsilon=0}. }[/math]
Since, for some function [math]\displaystyle{ \sigma : [t_0,t_1]\to \mathfrak{so}(3), }[/math] [math]\displaystyle{ \Theta^t(\epsilon) = \epsilon\sigma(t) + o(\epsilon) }[/math], as [math]\displaystyle{ \epsilon \to 0 }[/math],
[math]\displaystyle{ \delta \gamma (t) = \gamma(t)\sigma(t) \in T_{\gamma(t)}SO(3). }[/math]
See also
- D'Alembert principle
- Virtual work
References
- ↑ 1.0 1.1 Takhtajan, Leon A. (2017). "Part 1. Classical Mechanics" (PDF). Classical Field Theory. Department of Mathematics, Stony Brook University, Stony Brook, NY. http://www.math.stonybrook.edu/~kirillov/mat560-fall19/MAT%20560.pdf.
- ↑ Goldstein, H.; Poole, C. P.; Safko, J. L. (2001). Classical Mechanics (3rd ed.). Addison-Wesley. pp. 16. ISBN 978-0-201-65702-9.
- ↑ Torby, Bruce (1984). "Energy Methods". Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.
 |  |
