Tangent bundle

From HandWiki
Short description: Tangent spaces of a manifold
Informally, the tangent bundle of a manifold (which in this case is a circle) is obtained by considering all the tangent spaces (top), and joining them together in a smooth and non-overlapping manner (bottom).[note 1]

A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold [math]\displaystyle{ M }[/math] is a manifold [math]\displaystyle{ TM }[/math] which assembles all the tangent vectors in [math]\displaystyle{ M }[/math]. As a set, it is given by the disjoint union[note 1] of the tangent spaces of [math]\displaystyle{ M }[/math]. That is,

[math]\displaystyle{ \begin{align} TM &= \bigsqcup_{x \in M} T_xM \\ &= \bigcup_{x \in M} \left\{x\right\} \times T_xM \\ &= \bigcup_{x \in M} \left\{(x, y) \mid y \in T_xM\right\} \\ &= \left\{ (x, y) \mid x \in M,\, y \in T_xM \right\} \end{align} }[/math]

where [math]\displaystyle{ T_x M }[/math] denotes the tangent space to [math]\displaystyle{ M }[/math] at the point [math]\displaystyle{ x }[/math]. So, an element of [math]\displaystyle{ TM }[/math] can be thought of as a pair [math]\displaystyle{ (x,v) }[/math], where [math]\displaystyle{ x }[/math] is a point in [math]\displaystyle{ M }[/math] and [math]\displaystyle{ v }[/math] is a tangent vector to [math]\displaystyle{ M }[/math] at [math]\displaystyle{ x }[/math].

There is a natural projection

[math]\displaystyle{ \pi : TM \twoheadrightarrow M }[/math]

defined by [math]\displaystyle{ \pi(x, v) = x }[/math]. This projection maps each element of the tangent space [math]\displaystyle{ T_xM }[/math] to the single point [math]\displaystyle{ x }[/math].

The tangent bundle comes equipped with a natural topology (described in a section below). With this topology, the tangent bundle to a manifold is the prototypical example of a vector bundle (which is a fiber bundle whose fibers are vector spaces). A section of [math]\displaystyle{ TM }[/math] is a vector field on [math]\displaystyle{ M }[/math], and the dual bundle to [math]\displaystyle{ TM }[/math] is the cotangent bundle, which is the disjoint union of the cotangent spaces of [math]\displaystyle{ M }[/math]. By definition, a manifold [math]\displaystyle{ M }[/math] is parallelizable if and only if the tangent bundle is trivial. By definition, a manifold [math]\displaystyle{ M }[/math] is framed if and only if the tangent bundle [math]\displaystyle{ TM }[/math] is stably trivial, meaning that for some trivial bundle [math]\displaystyle{ E }[/math] the Whitney sum [math]\displaystyle{ TM\oplus E }[/math] is trivial. For example, the n-dimensional sphere Sn is framed for all n, but parallelizable only for n = 1, 3, 7 (by results of Bott-Milnor and Kervaire).

Role

One of the main roles of the tangent bundle is to provide a domain and range for the derivative of a smooth function. Namely, if [math]\displaystyle{ f:M\rightarrow N }[/math] is a smooth function, with [math]\displaystyle{ M }[/math] and [math]\displaystyle{ N }[/math] smooth manifolds, its derivative is a smooth function [math]\displaystyle{ Df:TM\rightarrow TN }[/math].

Topology and smooth structure

The tangent bundle comes equipped with a natural topology (not the disjoint union topology) and smooth structure so as to make it into a manifold in its own right. The dimension of [math]\displaystyle{ TM }[/math] is twice the dimension of [math]\displaystyle{ M }[/math].

Each tangent space of an n-dimensional manifold is an n-dimensional vector space. If [math]\displaystyle{ U }[/math] is an open contractible subset of [math]\displaystyle{ M }[/math], then there is a diffeomorphism [math]\displaystyle{ TU\to U\times\mathbb R^n }[/math] which restricts to a linear isomorphism from each tangent space [math]\displaystyle{ T_xU }[/math] to [math]\displaystyle{ \{x\}\times\mathbb R^n }[/math]. As a manifold, however, [math]\displaystyle{ TM }[/math] is not always diffeomorphic to the product manifold [math]\displaystyle{ M\times\mathbb R^n }[/math]. When it is of the form [math]\displaystyle{ M\times\mathbb R^n }[/math], then the tangent bundle is said to be trivial. Trivial tangent bundles usually occur for manifolds equipped with a 'compatible group structure'; for instance, in the case where the manifold is a Lie group. The tangent bundle of the unit circle is trivial because it is a Lie group (under multiplication and its natural differential structure). It is not true however that all spaces with trivial tangent bundles are Lie groups; manifolds which have a trivial tangent bundle are called parallelizable. Just as manifolds are locally modeled on Euclidean space, tangent bundles are locally modeled on [math]\displaystyle{ U\times\mathbb R^n }[/math], where [math]\displaystyle{ U }[/math] is an open subset of Euclidean space.

If M is a smooth n-dimensional manifold, then it comes equipped with an atlas of charts [math]\displaystyle{ (U_\alpha,\phi_\alpha) }[/math], where [math]\displaystyle{ U_\alpha }[/math] is an open set in [math]\displaystyle{ M }[/math] and

[math]\displaystyle{ \phi_\alpha: U_\alpha \to \mathbb R^n }[/math]

is a diffeomorphism. These local coordinates on [math]\displaystyle{ U_\alpha }[/math] give rise to an isomorphism [math]\displaystyle{ T_xM\rightarrow\mathbb R^n }[/math] for all [math]\displaystyle{ x\in U_\alpha }[/math]. We may then define a map

[math]\displaystyle{ \widetilde\phi_\alpha:\pi^{-1}\left(U_\alpha\right) \to \mathbb R^{2n} }[/math]

by

[math]\displaystyle{ \widetilde\phi_\alpha\left(x, v^i\partial_i\right) = \left(\phi_\alpha(x), v^1, \cdots, v^n\right) }[/math]

We use these maps to define the topology and smooth structure on [math]\displaystyle{ TM }[/math]. A subset [math]\displaystyle{ A }[/math] of [math]\displaystyle{ TM }[/math] is open if and only if

[math]\displaystyle{ \widetilde\phi_\alpha\left(A\cap \pi^{-1}\left(U_\alpha\right)\right) }[/math]

is open in [math]\displaystyle{ \mathbb R^{2n} }[/math] for each [math]\displaystyle{ \alpha. }[/math] These maps are homeomorphisms between open subsets of [math]\displaystyle{ TM }[/math] and [math]\displaystyle{ \mathbb R^{2n} }[/math] and therefore serve as charts for the smooth structure on [math]\displaystyle{ TM }[/math]. The transition functions on chart overlaps [math]\displaystyle{ \pi^{-1}\left(U_\alpha \cap U_\beta\right) }[/math] are induced by the Jacobian matrices of the associated coordinate transformation and are therefore smooth maps between open subsets of [math]\displaystyle{ \mathbb R^{2n} }[/math].

The tangent bundle is an example of a more general construction called a vector bundle (which is itself a specific kind of fiber bundle). Explicitly, the tangent bundle to an [math]\displaystyle{ n }[/math]-dimensional manifold [math]\displaystyle{ M }[/math] may be defined as a rank [math]\displaystyle{ n }[/math] vector bundle over [math]\displaystyle{ M }[/math] whose transition functions are given by the Jacobian of the associated coordinate transformations.

Examples

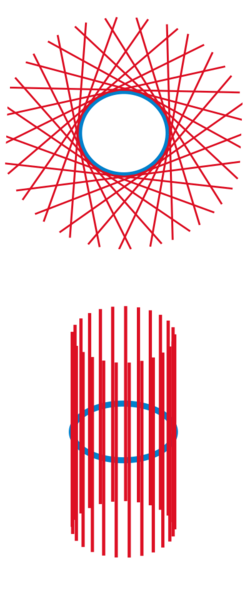
The simplest example is that of [math]\displaystyle{ \mathbb R^n }[/math]. In this case the tangent bundle is trivial: each [math]\displaystyle{ T_x \mathbf \mathbb R^n }[/math] is canonically isomorphic to [math]\displaystyle{ T_0 \mathbb R^n }[/math] via the map [math]\displaystyle{ \mathbb R^n \to \mathbb R^n }[/math] which subtracts [math]\displaystyle{ x }[/math], giving a diffeomorphism [math]\displaystyle{ T\mathbb R^n \to \mathbb R^n \times \mathbb R^n }[/math].

Another simple example is the unit circle, [math]\displaystyle{ S^1 }[/math] (see picture above). The tangent bundle of the circle is also trivial and isomorphic to [math]\displaystyle{ S^1\times\mathbb R }[/math]. Geometrically, this is a cylinder of infinite height.

The only tangent bundles that can be readily visualized are those of the real line [math]\displaystyle{ \mathbb R }[/math] and the unit circle [math]\displaystyle{ S^1 }[/math], both of which are trivial. For 2-dimensional manifolds the tangent bundle is 4-dimensional and hence difficult to visualize.

A simple example of a nontrivial tangent bundle is that of the unit sphere [math]\displaystyle{ S^2 }[/math]: this tangent bundle is nontrivial as a consequence of the hairy ball theorem. Therefore, the sphere is not parallelizable.

Vector fields

A smooth assignment of a tangent vector to each point of a manifold is called a vector field. Specifically, a vector field on a manifold [math]\displaystyle{ M }[/math] is a smooth map

[math]\displaystyle{ V\colon M \to TM }[/math]

such that [math]\displaystyle{ V(x) = (x,V_x) }[/math] with [math]\displaystyle{ V_x\in T_xM }[/math] for every [math]\displaystyle{ x\in M }[/math]. In the language of fiber bundles, such a map is called a section. A vector field on [math]\displaystyle{ M }[/math] is therefore a section of the tangent bundle of [math]\displaystyle{ M }[/math].

The set of all vector fields on [math]\displaystyle{ M }[/math] is denoted by [math]\displaystyle{ \Gamma(TM) }[/math]. Vector fields can be added together pointwise

[math]\displaystyle{ (V+W)_x = V_x + W_x }[/math]

and multiplied by smooth functions on M

[math]\displaystyle{ (fV)_x = f(x)V_x }[/math]

to get other vector fields. The set of all vector fields [math]\displaystyle{ \Gamma(TM) }[/math] then takes on the structure of a module over the commutative algebra of smooth functions on M, denoted [math]\displaystyle{ C^{\infty}(M) }[/math].

A local vector field on [math]\displaystyle{ M }[/math] is a local section of the tangent bundle. That is, a local vector field is defined only on some open set [math]\displaystyle{ U\subset M }[/math] and assigns to each point of [math]\displaystyle{ U }[/math] a vector in the associated tangent space. The set of local vector fields on [math]\displaystyle{ M }[/math] forms a structure known as a sheaf of real vector spaces on [math]\displaystyle{ M }[/math].

The above construction applies equally well to the cotangent bundle – the differential 1-forms on [math]\displaystyle{ M }[/math] are precisely the sections of the cotangent bundle [math]\displaystyle{ \omega \in \Gamma(T^*M) }[/math], [math]\displaystyle{ \omega: M \to T^*M }[/math] that associate to each point [math]\displaystyle{ x \in M }[/math] a 1-covector [math]\displaystyle{ \omega_x \in T^*_xM }[/math], which map tangent vectors to real numbers: [math]\displaystyle{ \omega_x : T_xM \to \R }[/math]. Equivalently, a differential 1-form [math]\displaystyle{ \omega \in \Gamma(T^*M) }[/math] maps a smooth vector field [math]\displaystyle{ X \in \Gamma(TM) }[/math] to a smooth function [math]\displaystyle{ \omega(X) \in C^{\infty}(M) }[/math].

Higher-order tangent bundles

Since the tangent bundle [math]\displaystyle{ TM }[/math] is itself a smooth manifold, the second-order tangent bundle can be defined via repeated application of the tangent bundle construction:

[math]\displaystyle{ T^2 M = T(TM).\, }[/math]

In general, the [math]\displaystyle{ k }[/math]th order tangent bundle [math]\displaystyle{ T^k M }[/math] can be defined recursively as [math]\displaystyle{ T\left(T^{k-1}M\right) }[/math].

A smooth map [math]\displaystyle{ f: M \rightarrow N }[/math] has an induced derivative, for which the tangent bundle is the appropriate domain and range [math]\displaystyle{ Df : TM \rightarrow TN }[/math]. Similarly, higher-order tangent bundles provide the domain and range for higher-order derivatives [math]\displaystyle{ D^k f : T^k M \to T^k N }[/math].

A distinct but related construction are the jet bundles on a manifold, which are bundles consisting of jets.

Canonical vector field on tangent bundle

On every tangent bundle [math]\displaystyle{ TM }[/math], considered as a manifold itself, one can define a canonical vector field [math]\displaystyle{ V:TM\rightarrow T^2M }[/math] as the diagonal map on the tangent space at each point. This is possible because the tangent space of a vector space W is naturally a product, [math]\displaystyle{ TW \cong W \times W, }[/math] since the vector space itself is flat, and thus has a natural diagonal map [math]\displaystyle{ W \to TW }[/math] given by [math]\displaystyle{ w \mapsto (w, w) }[/math] under this product structure. Applying this product structure to the tangent space at each point and globalizing yields the canonical vector field. Informally, although the manifold [math]\displaystyle{ M }[/math] is curved, each tangent space at a point [math]\displaystyle{ x }[/math], [math]\displaystyle{ T_x M \approx \mathbb{R}^n }[/math], is flat, so the tangent bundle manifold [math]\displaystyle{ TM }[/math] is locally a product of a curved [math]\displaystyle{ M }[/math] and a flat [math]\displaystyle{ \mathbb{R}^n. }[/math] Thus the tangent bundle of the tangent bundle is locally (using [math]\displaystyle{ \approx }[/math] for "choice of coordinates" and [math]\displaystyle{ \cong }[/math] for "natural identification"):

[math]\displaystyle{ T(TM) \approx T(M \times \mathbb{R}^n) \cong TM \times T(\mathbb{R}^n) \cong TM \times ( \mathbb{R}^n\times\mathbb{R}^n) }[/math]

and the map [math]\displaystyle{ TTM \to TM }[/math] is the projection onto the first coordinates:

[math]\displaystyle{ (TM \to M) \times (\mathbb{R}^n \times \mathbb{R}^n \to \mathbb{R}^n). }[/math]

Splitting the first map via the zero section and the second map by the diagonal yields the canonical vector field.

If [math]\displaystyle{ (x,v) }[/math] are local coordinates for [math]\displaystyle{ TM }[/math], the vector field has the expression

[math]\displaystyle{ V = \sum_i \left. v^i \frac{\partial}{\partial v^i} \right|_{(x,v)}. }[/math]

More concisely, [math]\displaystyle{ (x, v) \mapsto (x, v, 0, v) }[/math] – the first pair of coordinates do not change because it is the section of a bundle and these are just the point in the base space: the last pair of coordinates are the section itself. This expression for the vector field depends only on [math]\displaystyle{ v }[/math], not on [math]\displaystyle{ x }[/math], as only the tangent directions can be naturally identified.

Alternatively, consider the scalar multiplication function:

[math]\displaystyle{ \begin{cases} \mathbb{R} \times TM \to TM \\ (t,v) \longmapsto tv \end{cases} }[/math]

The derivative of this function with respect to the variable [math]\displaystyle{ \mathbb R }[/math] at time [math]\displaystyle{ t=1 }[/math] is a function [math]\displaystyle{ V:TM\rightarrow T^2M }[/math], which is an alternative description of the canonical vector field.

The existence of such a vector field on [math]\displaystyle{ TM }[/math] is analogous to the canonical one-form on the cotangent bundle. Sometimes [math]\displaystyle{ V }[/math] is also called the Liouville vector field, or radial vector field. Using [math]\displaystyle{ V }[/math] one can characterize the tangent bundle. Essentially, [math]\displaystyle{ V }[/math] can be characterized using 4 axioms, and if a manifold has a vector field satisfying these axioms, then the manifold is a tangent bundle and the vector field is the canonical vector field on it. See for example, De León et al.

Lifts

There are various ways to lift objects on [math]\displaystyle{ M }[/math] into objects on [math]\displaystyle{ TM }[/math]. For example, if [math]\displaystyle{ \gamma }[/math] is a curve in [math]\displaystyle{ M }[/math], then [math]\displaystyle{ \gamma' }[/math] (the tangent of [math]\displaystyle{ \gamma }[/math]) is a curve in [math]\displaystyle{ TM }[/math]. In contrast, without further assumptions on [math]\displaystyle{ M }[/math] (say, a Riemannian metric), there is no similar lift into the cotangent bundle.

The vertical lift of a function [math]\displaystyle{ f:M\rightarrow\mathbb R }[/math] is the function [math]\displaystyle{ f^\vee:TM\rightarrow\mathbb R }[/math] defined by [math]\displaystyle{ f^\vee=f\circ \pi }[/math], where [math]\displaystyle{ \pi:TM\rightarrow M }[/math] is the canonical projection.

See also

Notes

  1. ↑ 1.0 1.1 The disjoint union ensures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector. This is graphically illustrated in the accompanying picture for tangent bundle of circle S1, see Examples section: all tangents to a circle lie in the plane of the circle. In order to make them disjoint it is necessary to align them in a plane perpendicular to the plane of the circle.

References

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Tangent_bundle&oldid=3383023"