Point set triangulation

Two different triangulations of the same set of 9 points in the plane.

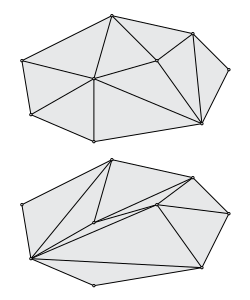
A triangulation of a set of points [math]\displaystyle{ \mathcal{P} }[/math] in the Euclidean space [math]\displaystyle{ \mathbb{R}^d }[/math] is a simplicial complex that covers the convex hull of [math]\displaystyle{ \mathcal{P} }[/math], and whose vertices belong to [math]\displaystyle{ \mathcal{P} }[/math]. In the plane (when [math]\displaystyle{ \mathcal{P} }[/math] is a set of points in [math]\displaystyle{ \mathbb{R}^2 }[/math]), triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of [math]\displaystyle{ \mathcal{P} }[/math] are vertices of its triangulations. In this case, a triangulation of a set of points [math]\displaystyle{ \mathcal{P} }[/math] in the plane can alternatively be defined as a maximal set of non-crossing edges between points of [math]\displaystyle{ \mathcal{P} }[/math]. In the plane, triangulations are special cases of planar straight-line graphs.

A particularly interesting kind of triangulations are the Delaunay triangulations. They are the geometric duals of Voronoi diagrams. The Delaunay triangulation of a set of points [math]\displaystyle{ \mathcal{P} }[/math] in the plane contains the Gabriel graph, the nearest neighbor graph and the minimal spanning tree of [math]\displaystyle{ \mathcal{P} }[/math].

Triangulations have a number of applications, and there is an interest to find the "good" triangulations of a given point set under some criteria as, for instance minimum-weight triangulations. Sometimes it is desirable to have a triangulation with special properties, e.g., in which all triangles have large angles (long and narrow ("splinter") triangles are avoided).

Given a set of edges that connect points of the plane, the problem to determine whether they contain a triangulation is NP-complete.

Regular triangulations

Some triangulations of a set of points [math]\displaystyle{ \mathcal{P}\subset\mathbb{R}^d }[/math] can be obtained by lifting the points of [math]\displaystyle{ \mathcal{P} }[/math] into [math]\displaystyle{ \mathbb{R}^{d+1} }[/math] (which amounts to add a coordinate [math]\displaystyle{ x_{d+1} }[/math] to each point of [math]\displaystyle{ \mathcal{P} }[/math]), by computing the convex hull of the lifted set of points, and by projecting the lower faces of this convex hull back on [math]\displaystyle{ \mathbb{R}^d }[/math]. The triangulations built this way are referred to as the regular triangulations of [math]\displaystyle{ \mathcal{P} }[/math]. When the points are lifted to the paraboloid of equation [math]\displaystyle{ x_{d+1} = x_1^2+\cdots+x_d^2 }[/math], this construction results in the Delaunay triangulation of [math]\displaystyle{ \mathcal{P} }[/math]. Note that, in order for this construction to provide a triangulation, the lower convex hull of the lifted set of points needs to be simplicial. In the case of Delaunay triangulations, this amounts to require that no [math]\displaystyle{ d+2 }[/math] points of [math]\displaystyle{ \mathcal{P} }[/math] lie in the same sphere.

Combinatorics in the plane

Every triangulation of any set [math]\displaystyle{ \mathcal{P} }[/math] of [math]\displaystyle{ n }[/math] points in the plane has [math]\displaystyle{ 2n - h - 2 }[/math] triangles and [math]\displaystyle{ 3n - h - 3 }[/math] edges where [math]\displaystyle{ h }[/math] is the number of points of [math]\displaystyle{ \mathcal{P} }[/math] in the boundary of the convex hull of [math]\displaystyle{ \mathcal{P} }[/math]. This follows from a straightforward Euler characteristic argument.

Algorithms to build triangulations in the plane

Triangle Splitting Algorithm : Find the convex hull of the point set [math]\displaystyle{ \mathcal{P} }[/math] and triangulate this hull as a polygon. Choose an interior point and draw edges to the three vertices of the triangle that contains it. Continue this process until all interior points are exhausted.

Incremental Algorithm : Sort the points of [math]\displaystyle{ \mathcal{P} }[/math] according to x-coordinates. The first three points determine a triangle. Consider the next point [math]\displaystyle{ p }[/math] in the ordered set and connect it with all previously considered points [math]\displaystyle{ \{p_1,..., p_k\} }[/math] which are visible to p. Continue this process of adding one point of [math]\displaystyle{ \mathcal{P} }[/math] at a time until all of [math]\displaystyle{ \mathcal{P} }[/math] has been processed.

Time complexity of various algorithms

The following table reports time complexity results for the construction of triangulations of point sets in the plane, under different optimality criteria, where [math]\displaystyle{ n }[/math] is the number of points.

		minimize	maximize
minimum	angle		[math]\displaystyle{ O(n \log n) }[/math] (Delaunay triangulation)
maximum		[math]\displaystyle{ O(n^2 \log n) }[/math]
minimum	area	[math]\displaystyle{ O(n^2) }[/math]	[math]\displaystyle{ O(n^2 \log n) }[/math]
maximum		[math]\displaystyle{ O(n^2 \log n) }[/math]
maximum	degree	NP-complete for degree of 7
maximum	eccentricity	[math]\displaystyle{ O(n^3) }[/math]
minimum	edge length	[math]\displaystyle{ O(n \log n) }[/math] (Closest pair of points problem)	NP-complete
maximum		[math]\displaystyle{ O(n^2) }[/math]	[math]\displaystyle{ O(n \log n) }[/math] (using the Convex hull)
sum of		NP-hard (Minimum-weight triangulation)
minimum	height		[math]\displaystyle{ O(n^2 \log n) }[/math]
maximum	slope	[math]\displaystyle{ O(n^3) }[/math]

See also

• Polygon triangulation

References

• Bern, M. (1993), "Edge insertion for optimal triangulations", Discrete and Computational Geometry 10 (1): 47–65, doi:10.1007/BF02573962 
• Chazelle, Bernard; Guibas, Leo J.; Lee, D. T. (1985). "The power of geometric duality". BIT (BIT Computer Science and Numerical Mathematics) 25 (1): 76–90. doi:10.1007/BF01934990. ISSN 0006-3835. http://www.cs.princeton.edu/~chazelle/pubs/PowerDuality.pdf. 
• de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2008). Computational Geometry: Algorithms and Applications (3 ed.). Springer-Verlag. http://www.cs.uu.nl/geobook/. 
• O'Rourke, Joseph (2011). Discrete and Computational Geometry (1 ed.). Princeton University Press. 
• Edelsbrunner, Herbert; Tan, Tiow Seng; Waupotitsch, Roman (1990). "An O(n2log n) time algorithm for the MinMax angle triangulation". Proceedings of the sixth annual symposium on Computational geometry. ACM. pp. 44–52. doi:10.1145/98524.98535. ISBN 0-89791-362-0. 
• Edelsbrunner, Herbert; Tan, Tiow Seng (1991). "A quadratic time algorithm for the minmax length triangulation". 32nd Annual Symposium on Foundations of Computer Science. pp. 414–423. doi:10.1109/SFCS.1991.185400. ISBN 0-8186-2445-0. 
• Fekete, Sándor P. (2012). "The Complexity of MaxMin Length Triangulation". arXiv:1208.0202v1 [cs.CG].CS1 maint: ref=harv (link)
• Jansen, Klaus (1992). "The Complexity of the Min-max Degree Triangulation Problem". 9th European Workshop on Computational Geometry. pp. 40–43. http://tizian.cs.uni-bonn.de/EuroCG93/j-cmmdt-93.pdf. 
• Lloyd, Errol Lynn (1977). "On triangulations of a set of points in the plane". 18th Annual Symposium on Foundations of Computer Science. 228–240. doi:10.1109/SFCS.1977.21. 
• Vassilev, Tzvetalin Simeonov (2005). Optimal Area Triangulation (PDF) (Ph.D.). University of Saskatchewan, Saskatoon. Archived from the original (PDF) on 2017-08-13. Retrieved 2013-06-15.CS1 maint: ref=harv (link)

de:Gitter (Geometrie)#Dreiecksgitter