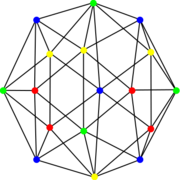
Errera graph

Errera graph
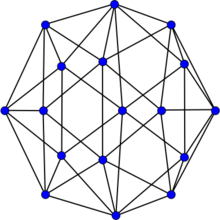The Errera graph
Named after	Alfred Errera
Vertices	17
Edges	45
Radius	3
Diameter	4
Girth	3
Automorphisms	20 (D10)
Chromatic number	4
Chromatic index	6
Properties	Planar Hamiltonian
Table of graphs and parameters

In the mathematical field of graph theory, the Errera graph is a graph with 17 vertices and 45 edges. Alfred Errera published it in 1921 as a counterexample to Kempe's erroneous proof of the four color theorem; it was named after Errera by (Hutchinson Wagon).

Properties

The Errera graph is planar and has chromatic number 4, chromatic index 6, radius 3, diameter 4 and girth 3. All its vertices are of degree 5 or 6 and it is a 5-vertex-connected graph and a 5-edge-connected graph.

The Errera graph is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 20, the group of symmetries of a decagon, including both rotations and reflections.

The characteristic polynomial of the Errera graph is [math]\displaystyle{ -(x^2-2 x-5) (x^2+x-1)^2 (x^3-4 x^2-9 x+10) (x^4+2 x^3-7 x^2-18 x-9)^2 }[/math].

The chromatic number of the Errera graph is 4.

The chromatic index of the Errera graph is 6.

The Errera graph is planar.

Application to the four color theorem

Tangled Kempe chains in the Errera graph.

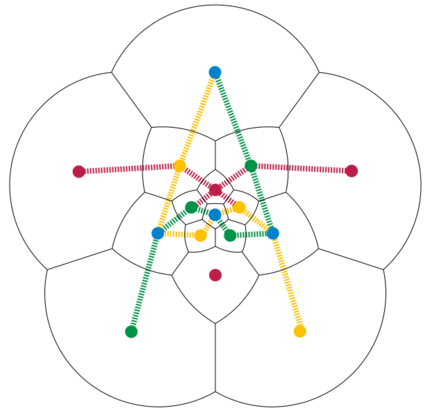
The four color theorem states that the vertices of every planar graph can be colored with four colors, so that no two adjacent vertices have equal colors. An erroneous proof was published in 1879 by Alfred Kempe, but it was discovered to be erroneous by 1890. The four color theorem was not given a valid proof until 1976. Kempe's proof can be translated into an algorithm to color planar graphs, which is also erroneous. Counterexamples to his proof were found in 1890 and 1896 (the Poussin graph), and later, the Fritsch graph and Soifer graph provided two smaller counterexamples. However, until the work of Errera, these counterexamples did not show that the whole coloring algorithm fails. Rather, they assumed that all but one vertex of the graph had already been colored, and showed that Kempe's method (which purportedly would modify the coloring to extend it to the whole graphs) failed in those precolored instances. The Errera graph, on the other hand, provides a counterexample to Kempe's entire method. When this method is run on the Errera graph, starting with no vertices colored, it can fail to find a valid coloring for the whole graph. Additionally, unlike the Poussin graph, all vertices in the Errera graph have degree five or more. Therefore, on this graph, it is impossible to avoid the problematic cases of Kempe's method by choosing lower-degree vertices.

The figure shows an example of how Kempe's proof can fail for this graph. In the figure, the adjacencies between regions of this map form the Errera graph, partially four-colored with the outer region uncolored. Kempe's erroneous proof follows the idea of extending partial colorings such as this one by recoloring Kempe chains, connected subgraphs that have only two colors. Any such chain can be recolored, preserving the validity of the coloring, by swapping its two colors on all vertices of the chain. Kempe's proof has different cases depending on whether the next vertex to be colored has three, four, or five neighbors and on how those neighbors are colored. In the case shown, the vertex to be colored next is the one corresponding to the outer region of the map. This region cannot be colored directly, because it already has neighbors of all four different colors. The blue and yellow neighbors are connected by a single Kempe chain (shown by the dashed yellow lines in the image), preventing a swap from making them both blue or both yellow and freeing a color. Similarly, the blue and green neighbors are connected by another Kempe chain (the dashed green lines). In such a case, Kempe's proof would try to simultaneously swap the colors on two Kempe chains, the left red-yellow chain and the right red-green chain (dashed red lines). The blue-green chain blocks the left red-yellow chain from reaching the right side of the graph, and the blue-yellow chain blocks the right red-green chain from reaching the left, so it would seem that simultaneously swapping the colors on these two chains is a safe operation. But because the blue-yellow and blue-green chains cross each other rather than staying separated, there is a region in the middle of the figure where the red-yellow and red-green chains can meet. When these two chains meet in the middle, the simultaneous swap causes adjacent yellow and green vertices in this middle area (such as the vertices represented by the upper yellow and green regions in the figure) to both become red, producing an invalid coloring.

Applications in chemistry

Chemical graph theory concerns the graph-theoretic structure of molecules and other clusters of atoms. Both the Errera graph itself and its dual graph are relevant in this context.

Atoms of metals such as gold can form clusters in which a central atom is surrounded by twelve more atoms, in the pattern of an icosahedron. Another, larger, type of cluster can be formed by coalescing two of these icosahedral clusters, so that the central atom of each cluster becomes one of the boundary atoms for the other cluster. The resulting cluster of 19 atoms has two interior atoms (the centers of the two icosahedra) with 17 atoms in the outer shell in the pattern of the Errera graph.

The dual graph of the Errera graph is a fullerene with 30 vertices, designated in the chemistry literature as C₃₀(D_5h) or F₃₀(D_5h) to indicate its symmetry and distinguish it from other 30-vertex fullerenes. This shape also plays a central role in the construction of higher-dimensional fullerenes.

External links

• Weisstein, Eric W.. "Errera graph". http://mathworld.wolfram.com/ErreraGraph.html.