Prüfer group

The Prüfer 2-group with presentation ⟨g_n: g_n+1² = g_n, g₁² = e⟩, illustrated as a subgroup of the unit circle in the complex plane

In mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p^∞-group, Z(p^∞), for a prime number p is the unique p-group in which every element has p different p-th roots.

The Prüfer p-groups are countable abelian groups that are important in the classification of infinite abelian groups: they (along with the group of rational numbers) form the smallest building blocks of all divisible groups.

The groups are named after Heinz Prüfer, a German mathematician of the early 20th century.

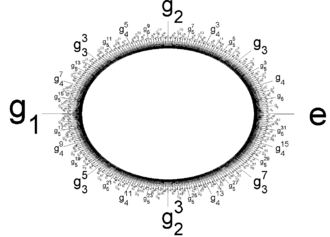
Constructions of Z(p^∞)

The Prüfer p-group may be identified with the subgroup of the circle group, U(1), consisting of all pⁿ-th roots of unity as n ranges over all non-negative integers:

[math]\displaystyle{ \mathbf{Z}(p^\infty)=\{\exp(2\pi i m/p^n) \mid 0 \leq m \lt p^n,\,n\in \mathbf{Z}^+\} = \{z\in\mathbf{C} \mid z^{(p^n)}=1 \text{ for some } n\in \mathbf{Z}^+\}.\; }[/math]

The group operation here is the multiplication of complex numbers.

There is a presentation

[math]\displaystyle{ \mathbf{Z}(p^\infty) = \langle\, g_1, g_2, g_3, \ldots \mid g_1^p = 1, g_2^p = g_1, g_3^p = g_2, \dots\,\rangle. }[/math]

Here, the group operation in Z(p^∞) is written as multiplication.

Alternatively and equivalently, the Prüfer p-group may be defined as the Sylow p-subgroup of the quotient group Q/Z, consisting of those elements whose order is a power of p:

[math]\displaystyle{ \mathbf{Z}(p^\infty) = \mathbf{Z}[1/p]/\mathbf{Z} }[/math]

(where Z[1/p] denotes the group of all rational numbers whose denominator is a power of p, using addition of rational numbers as group operation).

For each natural number n, consider the quotient group Z/pⁿZ and the embedding Z/pⁿZ → Z/pⁿ⁺¹Z induced by multiplication by p. The direct limit of this system is Z(p^∞):

[math]\displaystyle{ \mathbf{Z}(p^\infty) = \varinjlim \mathbf{Z}/p^n \mathbf{Z} . }[/math]

If we perform the direct limit in the category of topological groups, then we need to impose a topology on each of the [math]\displaystyle{ \mathbf{Z}/p^n \mathbf{Z} }[/math], and take the final topology on [math]\displaystyle{ \mathbf{Z}(p^\infty) }[/math]. If we wish for [math]\displaystyle{ \mathbf{Z}(p^\infty) }[/math] to be Hausdorff, we must impose the discrete topology on each of the [math]\displaystyle{ \mathbf{Z}/p^n \mathbf{Z} }[/math], resulting in [math]\displaystyle{ \mathbf{Z}(p^\infty) }[/math] to have the discrete topology.

We can also write

[math]\displaystyle{ \mathbf{Z}(p^\infty)=\mathbf{Q}_p/\mathbf{Z}_p }[/math]

where Q_p denotes the additive group of p-adic numbers and Z_p is the subgroup of p-adic integers.

Properties

The complete list of subgroups of the Prüfer p-group Z(p^∞) = Z[1/p]/Z is:

[math]\displaystyle{ 0 \subsetneq \left({1 \over p}\mathbf{Z}\right)/\mathbf{Z} \subsetneq \left({1 \over p^2}\mathbf{Z}\right)/\mathbf{Z} \subsetneq \left({1 \over p^3}\mathbf{Z}\right)/\mathbf{Z} \subsetneq \cdots \subsetneq \mathbf{Z}(p^\infty) }[/math]

Here, each [math]\displaystyle{ \left({1 \over p^n}\mathbf{Z}\right)/\mathbf{Z} }[/math] is a cyclic subgroup of Z(p^∞) with pⁿ elements; it contains precisely those elements of Z(p^∞) whose order divides pⁿ and corresponds to the set of pⁿ-th roots of unity.

The Prüfer p-groups are the only infinite groups whose subgroups are totally ordered by inclusion. This sequence of inclusions expresses the Prüfer p-group as the direct limit of its finite subgroups. As there is no maximal subgroup of a Prüfer p-group, it is its own Frattini subgroup.

Given this list of subgroups, it is clear that the Prüfer p-groups are indecomposable (cannot be written as a direct sum of proper subgroups). More is true: the Prüfer p-groups are subdirectly irreducible. An abelian group is subdirectly irreducible if and only if it is isomorphic to a finite cyclic p-group or to a Prüfer group.

The Prüfer p-group is the unique infinite p-group that is locally cyclic (every finite set of elements generates a cyclic group). As seen above, all proper subgroups of Z(p^∞) are finite. The Prüfer p-groups are the only infinite abelian groups with this property.

The Prüfer p-groups are divisible. They play an important role in the classification of divisible groups; along with the rational numbers they are the simplest divisible groups. More precisely: an abelian group is divisible if and only if it is the direct sum of a (possibly infinite) number of copies of Q and (possibly infinite) numbers of copies of Z(p^∞) for every prime p. The (cardinal) numbers of copies of Q and Z(p^∞) that are used in this direct sum determine the divisible group up to isomorphism.

As an abelian group (that is, as a Z-module), Z(p^∞) is Artinian but not Noetherian. It can thus be used as a counterexample against the idea that every Artinian module is Noetherian (whereas every Artinian ring is Noetherian).

The endomorphism ring of Z(p^∞) is isomorphic to the ring of p-adic integers Z_p.

In the theory of locally compact topological groups the Prüfer p-group (endowed with the discrete topology) is the Pontryagin dual of the compact group of p-adic integers, and the group of p-adic integers is the Pontryagin dual of the Prüfer p-group.

See also

• p-adic integers, which can be defined as the inverse limit of the finite subgroups of the Prüfer p-group.
• Dyadic rational, rational numbers of the form a/2^b. The Prüfer 2-group can be viewed as the dyadic rationals modulo 1.
• Cyclic group (finite analogue)
• Circle group (uncountably infinite analogue)

References

• Jacobson, Nathan (2009). Basic algebra. 2 (2nd ed.). Dover. ISBN 978-0-486-47187-7. 
• Pierre Antoine Grillet (2007). Abstract algebra. Springer. ISBN 978-0-387-71567-4. 
• Kaplansky, Irving (1965). Infinite Abelian Groups. University of Michigan Press. 
• Hazewinkel, Michiel, ed. (2001), "Quasi-cyclic group", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Q/q076440