Qvist's theorem

Qvist's theorem on finite ovals

In projective geometry, Qvist's theorem, named after the Finnish mathematician Bertil Qvist (de), is a statement on ovals in finite projective planes. Standard examples of ovals are non-degenerate (projective) conic sections. The theorem gives an answer to the question How many tangents to an oval can pass through a point in a finite projective plane? The answer depends essentially upon the order (number of points on a line −1) of the plane.

Definition of an oval

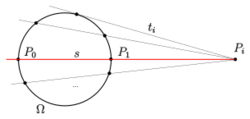
• In a projective plane a set Ω of points is called an oval, if:

1. Any line l meets Ω in at most two points, and
2. For any point P ∈ Ω there exists exactly one tangent line t through P, i.e., t ∩ Ω = {P}.

When |l ∩ Ω | = 0 the line l is an exterior line (or passant), if |l ∩ Ω| = 1 a tangent line and if |l ∩ Ω| = 2 the line is a secant line.

For finite planes (i.e. the set of points is finite) we have a more convenient characterization:

• For a finite projective plane of order n (i.e. any line contains n + 1 points) a set Ω of points is an oval if and only if |Ω| = n + 1 and no three points are collinear (on a common line).

Statement and proof of Qvist's theorem

Qvist's theorem

Let Ω be an oval in a finite projective plane of order n.

(a) If n is odd,

every point P ∉ Ω is incident with 0 or 2 tangents.

(b) If n is even,

there exists a point N, the nucleus or knot, such that, the set of tangents to oval Ω is the pencil of all lines through N.

Qvist's theorem: to the proof in case of n odd

Qvist's theorem: to the proof in case of n even

Proof

(a) Let t_R be the tangent to Ω at point R and let P₁, ... , P_n be the remaining points of this line. For each i, the lines through P_i partition Ω into sets of cardinality 2 or 1 or 0. Since the number |Ω| = n + 1 is even, for any point P_i, there must exist at least one more tangent through that point. The total number of tangents is n + 1, hence, there are exactly two tangents through each P_i, t_R and one other. Thus, for any point P not in oval Ω, if P is on any tangent to Ω it is on exactly two tangents.

(b) Let s be a secant, s ∩ Ω = {P₀, P₁} and s= {P₀, P₁,...,P_n}. Because |Ω| = n + 1 is odd, through any P_i, i = 2,...,n, there passes at least one tangent t_i. The total number of tangents is n + 1. Hence, through any point P_i for i = 2,...,n there is exactly one tangent. If N is the point of intersection of two tangents, no secant can pass through N. Because n + 1, the number of tangents, is also the number of lines through any point, any line through N is a tangent.

Example in a pappian plane of even order

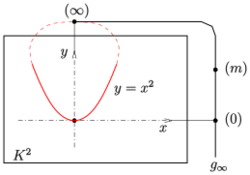
Using inhomogeneous coordinates over a field K, |K| = n even, the set

Ω₁ = {(x, y) | y = x²} ∪ {(∞)},

the projective closure of the parabola y = x², is an oval with the point N = (0) as nucleus (see image), i.e., any line y = c, with c ∈ K, is a tangent.

Definition and property of hyperovals

• Any oval Ω in a finite projective plane of even order n has a nucleus N.

The point set Ω := Ω ∪ {N} is called a hyperoval or (n + 2)-arc. (A finite oval is an (n + 1)-arc.)

One easily checks the following essential property of a hyperoval:

• For a hyperoval Ω and a point R ∈ Ω the pointset Ω \ {R} is an oval.

projective conic section Ω₁

This property provides a simple means of constructing additional ovals from a given oval.

Example

For a projective plane over a finite field K, |K| = n even and n > 4, the set

Ω₁ = {(x, y) | y = x²} ∪ {(∞)} is an oval (conic section) (see image),

Ω₁ = {(x, y) | y = x²} ∪ {(0), (∞)} is a hyperoval and

Ω₂ = {(x, y) | y = x²} ∪ {(0)} is another oval that is not a conic section. (Recall that a conic section is determined uniquely by 5 points.)

References

• Beutelspacher, Albrecht; Rosenbaum, Ute (1998), Projective Geometry / from foundations to applications, Cambridge University Press, ISBN 978-0-521-48364-3 
• Dembowski, Peter (1968), Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, ISBN 3-540-61786-8, https://archive.org/details/finitegeometries0000demb 

External links

• E. Hartmann: Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes. Skript, TH Darmstadt (PDF; 891 kB), p. 40.