Rayleigh's equation (fluid dynamics)

Example of a parallel shear flow.

In fluid dynamics, Rayleigh's equation or Rayleigh stability equation is a linear ordinary differential equation to study the hydrodynamic stability of a parallel, incompressible and inviscid shear flow. The equation is:

[math]\displaystyle{ (U-c) (\varphi'' - k^2 \varphi) - U'' \varphi=0, }[/math]

with [math]\displaystyle{ U(z) }[/math] the flow velocity of the steady base flow whose stability is to be studied and [math]\displaystyle{ z }[/math] is the cross-stream direction (i.e. perpendicular to the flow direction). Further [math]\displaystyle{ \varphi(z) }[/math] is the complex valued amplitude of the infinitesimal streamfunction perturbations applied to the base flow, [math]\displaystyle{ k }[/math] is the wavenumber of the perturbations and [math]\displaystyle{ c }[/math] is the phase speed with which the perturbations propagate in the flow direction. The prime denotes differentiation with respect to [math]\displaystyle{ z. }[/math]

Background

The equation is named after Lord Rayleigh, who introduced it in 1880. The Orr–Sommerfeld equation – introduced later, for the study of stability of parallel viscous flow – reduces to Rayleigh's equation when the viscosity is zero.

Rayleigh's equation, together with appropriate boundary conditions, most often poses an eigenvalue problem. For given (real-valued) wavenumber [math]\displaystyle{ k }[/math] and mean flow velocity [math]\displaystyle{ U(z), }[/math] the eigenvalues are the phase speeds [math]\displaystyle{ c, }[/math] and the eigenfunctions are the associated streamfunction amplitudes [math]\displaystyle{ \varphi(z). }[/math] In general, the eigenvalues form a continuous spectrum. In certain cases there may further be a discrete spectrum of complex conjugate pairs of [math]\displaystyle{ c. }[/math] Since the wavenumber [math]\displaystyle{ k }[/math] occurs only as a square [math]\displaystyle{ k^2 }[/math] in Rayleigh's equation, a solution (i.e. [math]\displaystyle{ \varphi(z) }[/math] and [math]\displaystyle{ c }[/math]) for wavenumber [math]\displaystyle{ +k }[/math] is also a solution for the wavenumber [math]\displaystyle{ -k. }[/math]

Rayleigh's equation only concerns two-dimensional perturbations to the flow. From Squire's theorem it follows that the two-dimensional perturbations are less stable than three-dimensional perturbations.

Kelvin's cat's eye pattern of streamlines near a critical layer.

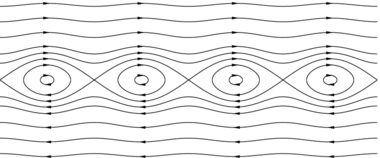
If a real-valued phase speed [math]\displaystyle{ c }[/math] is in between the minimum and maximum of [math]\displaystyle{ U(z), }[/math] the problem has so-called critical layers near [math]\displaystyle{ z=z_\mathrm{crit} }[/math] where [math]\displaystyle{ U(z_\mathrm{crit})=c. }[/math] At the critical layers Rayleigh's equation becomes singular. These were first being studied by Lord Kelvin, also in 1880. His solution gives rise to a so-called cat's eye pattern of streamlines near the critical layer, when observed in a frame of reference moving with the phase speed [math]\displaystyle{ c. }[/math]

Derivation

Consider a parallel shear flow [math]\displaystyle{ U(z) }[/math] in the [math]\displaystyle{ x }[/math] direction, which varies only in the cross-flow direction [math]\displaystyle{ z. }[/math] The stability of the flow is studied by adding small perturbations to the flow velocity [math]\displaystyle{ u(x,z,t) }[/math] and [math]\displaystyle{ w(x,z,t) }[/math] in the [math]\displaystyle{ x }[/math] and [math]\displaystyle{ z }[/math] directions, respectively. The flow is described using the incompressible Euler equations, which become after linearization – using velocity components [math]\displaystyle{ U(z)+u(x,z,t) }[/math] and [math]\displaystyle{ w(x,z,t): }[/math]

[math]\displaystyle{ \begin{align} &\partial_t u + U \, \partial_x u + w\, U' = -\frac 1 \rho \partial_x p, \\ &\partial_t w + U \, \partial_x w = -\frac 1 \rho \partial_z p \qquad \text{and} \\ &\partial_x u + \partial_z w = 0, \end{align} }[/math]

with [math]\displaystyle{ \partial_t }[/math] the partial derivative operator with respect to time, and similarly [math]\displaystyle{ \partial_x }[/math] and [math]\displaystyle{ \partial_z }[/math] with respect to [math]\displaystyle{ x }[/math] and [math]\displaystyle{ z. }[/math] The pressure fluctuations [math]\displaystyle{ p(x,z,t) }[/math] ensure that the continuity equation [math]\displaystyle{ \partial_x u + \partial_z w = 0 }[/math] is fulfilled. The fluid density is denoted as [math]\displaystyle{ \rho }[/math] and is a constant in the present analysis. The prime [math]\displaystyle{ U' }[/math] denotes differentiation of [math]\displaystyle{ U(z) }[/math] with respect to its argument [math]\displaystyle{ z. }[/math]

The flow oscillations [math]\displaystyle{ u }[/math] and [math]\displaystyle{ w }[/math] are described using a streamfunction [math]\displaystyle{ \psi(x,z,t), }[/math] ensuring that the continuity equation is satisfied:

[math]\displaystyle{ u=+\partial_z\psi \quad \text{ and } \quad w=-\partial_x\psi. }[/math]

Taking the [math]\displaystyle{ z }[/math]- and [math]\displaystyle{ x }[/math]-derivatives of the [math]\displaystyle{ x }[/math]- and [math]\displaystyle{ z }[/math]-momentum equation, and thereafter subtracting the two equations, the pressure [math]\displaystyle{ p }[/math] can be eliminated:

[math]\displaystyle{ \partial_t \left( \partial_x^2 \psi + \partial_z^2 \psi \right) + U\, \partial_x \left( \partial_x^2 \psi + \partial_z^2 \psi \right) - U''\, \partial_x \psi = 0, }[/math]

which is essentially the vorticity transport equation, [math]\displaystyle{ \partial_x^2\psi +\partial_z^2\psi }[/math] being (minus) the vorticity.

Next, sinusoidal fluctuations are considered:

[math]\displaystyle{ \psi(x,z,t) = \Re\left\{ \varphi(z)\, \exp(ik( x - ct)) \right\}, }[/math]

with [math]\displaystyle{ \varphi(z) }[/math] the complex-valued amplitude of the streamfunction oscillations, while [math]\displaystyle{ i }[/math] is the imaginary unit ([math]\displaystyle{ i^2=-1 }[/math]) and [math]\displaystyle{ \Re\left\{\cdot\right\} }[/math] denotes the real part of the expression between the brackets. Using this in the vorticity transport equation, Rayleigh's equation is obtained.

The boundary conditions for flat impermeable walls follow from the fact that the streamfunction is a constant at them. So at impermeable walls the streamfunction oscillations are zero, i.e. [math]\displaystyle{ \varphi=0. }[/math] For unbounded flows the common boundary conditions are that [math]\displaystyle{ \lim_{z\to\pm\infty}\varphi(z)=0. }[/math]

References

• Craik, A.D.D. (1988), Wave interactions and fluid flows, Cambridge University Press, ISBN 0-521-36829-4 
• Criminale, W.O.; Jackson, T.L.; Joslin, R.D. (2003), Theory and computation of hydrodynamic stability, Cambridge University Press, ISBN 978-0-521-63200-3 
• Drazin, P.G. (2002), Introduction to hydrodynamic stability, Cambridge University Press, ISBN 0-521-00965-0 
• Hirota, M.; Morrison, P.J.; Hattori, Y. (2014), "Variational necessary and sufficient stability conditions for inviscid shear flow", Proceedings of the Royal Society, A 470 (20140322): 23 pp, doi:10.1098/rspa.2014.0322, PMID 25484600, Bibcode: 2014RSPSA.47040322H 
• Kelvin, Lord (W. Thomson) (1880), "On a disturbing infinity in Lord Rayleigh's solution for waves in a plane vortex stratum", Nature 23 (576): 45–6, doi:10.1038/023045a0, Bibcode: 1880Natur..23...45. 
• Rayleigh, Lord (J.W. Strutt) (1880), "On the stability, or instability, of certain fluid motions", Proceedings of the London Mathematical Society 11: 57–70