Rectangular lattice
The rectangular lattice and rhombic lattice (or centered rectangular lattice) constitute two of the five two-dimensional Bravais lattice types.[1] The symmetry categories of these lattices are wallpaper groups pmm and cmm respectively. The conventional translation vectors of the rectangular lattices form an angle of 90° and are of unequal lengths.
Bravais lattices
There are two rectangular Bravais lattices: primitive rectangular and centered rectangular (also rhombic).
| Bravais lattice | Rectangular | Centered rectangular |
|---|---|---|
| Pearson symbol | op | oc |
| Standard unit cell | 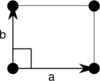
|
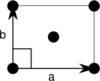
|
| Rhombic unit cell | 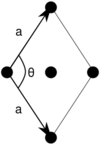
|
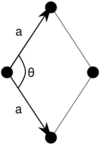
|
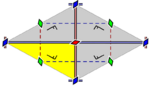
The primitive rectangular lattice can also be described by a centered rhombic unit cell, while the centered rectangular lattice can also be described by a primitive rhombic unit cell. Note that the length [math]\displaystyle{ a }[/math] in the lower row is not the same as in the upper row. For the first column above, [math]\displaystyle{ a }[/math] of the second row equals [math]\displaystyle{ \sqrt{a^2+b^2} }[/math] of the first row, and for the second column it equals [math]\displaystyle{ \frac{1}{2} \sqrt{a^2+b^2} }[/math].
Crystal classes
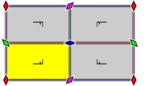
The rectangular lattice class names, Schönflies notation, Hermann-Mauguin notation, orbifold notation, Coxeter notation, and wallpaper groups are listed in the table below.
| Geometric class, point group | Arithmetic class |
Wallpaper groups | ||||
|---|---|---|---|---|---|---|
| Schön. | Intl | Orb. | Cox. | |||
| D1 | m | (*) | [ ] | Along | pm (**) |
pg (××) |
| Between | cm (*×) |
|||||
| D2 | 2mm | (*22) | [2] | Along | pmm (*2222) |
pmg (22*) |
| Between | cmm (2*22) |
pgg (22×) | ||||
References
 |