Regular skew apeirohedron

In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron, with either skew regular faces or skew regular vertex figures.
History
According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to finite regular skew polyhedra in 4-dimensions, and infinite regular skew apeirohedra in 3-dimensions (described here).
Coxeter identified 3 forms, with planar faces and skew vertex figures, two are complements of each other. They are all named with a modified Schläfli symbol {l,m|n}, where there are l-gonal faces, m faces around each vertex, with holes identified as n-gonal missing faces.
Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure, m l-gons around a vertex, and n-gonal holes. Their vertex figures are skew polygons, zig-zagging between two planes.
The regular skew polyhedra, represented by {l,m|n}, follow this equation:
- 2 sin(π/l) · sin(π/m) = cos(π/n)
Regular skew apeirohedra of Euclidean 3-space
The three Euclidean solutions in 3-space are {4,6|4}, {6,4|4}, and {6,6|3}. John Conway named them mucube, muoctahedron, and mutetrahedron respectively for multiple cube, octahedron, and tetrahedron.[1]
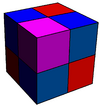
- Mucube: {4,6|4}: 6 squares about each vertex (related to cubic honeycomb, constructed by cubic cells, removing two opposite faces from each, and linking sets of six together around a faceless cube.)
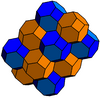
- Muoctahedron: {6,4|4}: 4 hexagons about each vertex (related to bitruncated cubic honeycomb, constructed by truncated octahedron with their square faces removed and linking hole pairs of holes together.)
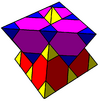
- Mutetrahedron: {6,6|3}: 6 hexagons about each vertex (related to quarter cubic honeycomb, constructed by truncated tetrahedron cells, removing triangle faces, and linking sets of four around a faceless tetrahedron.)
Coxeter gives these regular skew apeirohedra {2q,2r|p} with extended chiral symmetry [[(p,q,p,r)]+] which he says is isomorphic to his abstract group (2q,2r|2,p). The related honeycomb has the extended symmetry [[(p,q,p,r)]].[2]
| Coxeter group symmetry |
Apeirohedron {p,q|l} |
Image | Face {p} |
Hole {l} |
Vertex figure |
Related honeycomb | |
|---|---|---|---|---|---|---|---|
[[4,3,4]] [[4,3,4]+] |
{4,6|4} Mucube |
 animation |
100px | 100px | 100px | t0,3{4,3,4} |
|
| {6,4|4} Muoctahedron |
 animation |
100px | 100px | 2t{4,3,4} |
| ||
[[3[4]]] [[3[4]]+] |
{6,6|3} Mutetrahedron |
 animation |
100px | 100px | 100px | q{4,3,4} |
|
Regular skew apeirohedra in hyperbolic 3-space

In 1967, C. W. L. Garner identified 31 hyperbolic skew apeirohedra with regular skew polygon vertex figures, found in a similar search to the 3 above from Euclidean space.[3]
These represent 14 compact and 17 paracompact regular skew polyhedra in hyperbolic space, constructed from the symmetry of a subset of linear and cyclic Coxeter groups graphs of the form (p,q,p,r), These define regular skew polyhedra {2q,2r|p} and dual {2r,2q|p}. For the special case of linear graph groups r = 2, this represents the Coxeter group [p,q,p]. It generates regular skews {2q,4|p} and {4,2q|p}. All of these exist as a subset of faces of the convex uniform honeycombs in hyperbolic space.
The skew apeirohedron shares the same antiprism vertex figure with the honeycomb, but only the zig-zag edge faces of the vertex figure are realized, while the other faces make holes.
| Coxeter group |
Apeirohedron {p,q|l} |
Face {p} |
Hole {l} |
Honeycomb | Vertex figure |
Apeirohedron {p,q|l} |
Face {p} |
Hole {l} |
Honeycomb | Vertex figure | |
|---|---|---|---|---|---|---|---|---|---|---|---|
[3,5,3] |
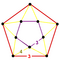
{10,4|3} |  |
60px | 2t{3,5,3} |
60px | {4,10|3} | 60px | 60px | t0,3{3,5,3} |
| |
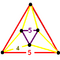
[5,3,5] |
{6,4|5} | 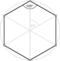 |
60px | 2t{5,3,5} |
60px | {4,6|5} | 60px | 60px | t0,3{5,3,5} |
| |
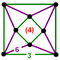
[(4,3,3,3)] |
{8,6|3} | 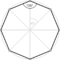 |
60px | ct{(4,3,3,3)} |
60px | {6,8|3} | 60px | 60px | ct{(3,3,4,3)} |
| |
[(5,3,3,3)] |
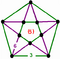
{10,6|3} |  |
60px | ct{(5,3,3,3)} |
60px | {6,10|3} | 60px | 60px | ct{(3,3,5,3)} |
| |
[(4,3,4,3)] |
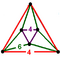
{8,8|3} |  |
60px | ct{(4,3,4,3)} |
60px | {6,6|4} | 60px | 60px | ct{(3,4,3,4)} |
| |
[(5,3,4,3)] |
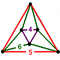
{8,10|3} |  |
60px | ct{(4,3,5,3)} |
60px | {10,8|3} | 60px | 60px | ct{(5,3,4,3)} |
| |
[(5,3,5,3)] |
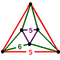
{10,10|3} |  |
60px | ct{(5,3,5,3)} |
60px | {6,6|5} | 60px | 60px | ct{(3,5,3,5)} |
|
| Coxeter group |
Apeirohedron {p,q|l} |
Face {p} |
Hole {l} |
Honeycomb | Vertex figure |
Apeirohedron {p,q|l} |
Face {p} |
Hole {l} |
Honeycomb | Vertex figure | |
|---|---|---|---|---|---|---|---|---|---|---|---|
[4,4,4] |
{8,4|4} |  |
60px | 2t{4,4,4} |
60px | {4,8|4} | 60px | 60px | t0,3{4,4,4} |

| |
[3,6,3] |
{12,4|3} | 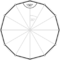 |
60px | 2t{3,6,3} |
60px | {4,12|3} | 60px | 60px | t0,3{3,6,3} |
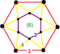
| |
[6,3,6] |
{6,4|6} | 60px | 60px | 2t{6,3,6} |
60px | {4,6|6} | 60px | 60px | t0,3{6,3,6} |

| |
[(4,4,4,3)] |
{8,6|4} |  |
60px | ct{(4,4,3,4)} |
60px | {6,8|4} | 60px | 60px | ct{(3,4,4,4)} |

| |
[(4,4,4,4)] |
{8,8|4} |  |
60px | q{4,4,4} |

| ||||||
[(6,3,3,3)] |
{12,6|3} |  |
60px | ct{(6,3,3,3)} |
60px | {6,12|3} | 60px | 60px | ct{(3,3,6,3)} |

| |
[(6,3,4,3)] |
{12,8|3} |  |
60px | ct{(6,3,4,3)} |
60px | {8,12|3} | 60px | 60px | ct{(4,3,6,3)} |

| |
[(6,3,5,3)] |
{12,10|3} |  |
60px | ct{(6,3,5,3)} |
60px | {10,12|3} | 60px | 60px | ct{(5,3,6,3)} |

| |
[(6,3,6,3)] |
{12,12|3} |  |
60px | ct{(6,3,6,3)} |
60px | {6,6|6} | 60px | 60px | ct{(3,6,3,6)} |
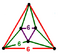
|
See also
References
- ↑ The Symmetry of Things, 2008, Chapter 23 Objects with Primary Symmetry, Infinite Platonic Polyhedra, pp. 333–335
- ↑ Coxeter, Regular and Semi-Regular Polytopes II 2.34)
- ↑ Garner, C. W. L. Regular Skew Polyhedra in Hyperbolic Three-Space. Can. J. Math. 19, 1179–1186, 1967. [1] Note: His paper says there are 32, but one is self-dual, leaving 31.
- Petrie–Coxeter Maps Revisited PDF, Isabel Hubard, Egon Schulte, Asia Ivic Weiss, 2005
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5,
- Peter McMullen, Four-Dimensional Regular Polyhedra, Discrete & Computational Geometry September 2007, Volume 38, Issue 2, pp 355–387
- Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 2) H.S.M. Coxeter, "The Regular Sponges, or Skew Polyhedra", Scripta Mathematica 6 (1939) 240–244.
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33–62, 1937.
 |
