Residual neural network

A residual neural network (also referred to as a residual network or ResNet)[1] is a deep learning architecture in which the layers learn residual functions with reference to the layer inputs. It was developed in 2015 for image recognition, and won the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) of that year.[2][3]
As a point of terminology, "residual connection" refers to the specific architectural motif of , where is an arbitrary neural network module. The motif had been used previously (see §History for details). However, the publication of ResNet made it widely popular for feedforward networks, appearing in neural networks that are seemingly unrelated to ResNet.
The residual connection stabilizes the training and convergence of deep neural networks with hundreds of layers, and is a common motif in deep neural networks, such as transformer models (e.g., BERT, and GPT models such as ChatGPT), the AlphaGo Zero system, the AlphaStar system, and the AlphaFold system.
Mathematics
Residual connection
In a multilayer neural network model, consider a subnetwork with a certain number of stacked layers (e.g., 2 or 3). Denote the underlying function performed by this subnetwork as , where is the input to the subnetwork. Residual learning re-parameterizes this subnetwork and lets the parameter layers represent a "residual function" . The output of this subnetwork is then represented as:
The operation of "" is implemented via a "skip connection" that performs an identity mapping to connect the input of the subnetwork with its output. This connection is referred to as a "residual connection" in later work. The function is often represented by matrix multiplication interlaced with activation functions and normalization operations (e.g., batch normalization or layer normalization). As a whole, one of these subnetworks is referred to as a "residual block".[1] A deep residual network is constructed by simply stacking these blocks.
Long short-term memory (LSTM) has a memory mechanism that serves as a residual connection.[4] In an LSTM without a forget gate, an input is processed by a function and added to a memory cell , resulting in . An LSTM with a forget gate essentially functions as a highway network.
To stabilize the variance of the layers' inputs, it is recommended to replace the residual connections with , where is the total number of residual layers.[5]
Projection connection
If the function is of type where , then is undefined. To handle this special case, a projection connection is used:
where is typically a linear projection, defined by where is a matrix. The matrix is trained via backpropagation, as is any other parameter of the model.
Signal propagation
The introduction of identity mappings facilitates signal propagation in both forward and backward paths.[6]
Forward propagation
If the output of the -th residual block is the input to the -th residual block (assuming no activation function between blocks), then the -th input is:
Applying this formulation recursively, e.g.:
yields the general relationship:
where is the index of a residual block and is the index of some earlier block. This formulation suggests that there is always a signal that is directly sent from a shallower block to a deeper block .
Backward propagation
The residual learning formulation provides the added benefit of mitigating the vanishing gradient problem to some extent. However, it is crucial to acknowledge that the vanishing gradient issue is not the root cause of the degradation problem, which is tackled through the use of normalization. To observe the effect of residual blocks on backpropagation, consider the partial derivative of a loss function with respect to some residual block input . Using the equation above from forward propagation for a later residual block :[6]
This formulation suggests that the gradient computation of a shallower layer, , always has a later term that is directly added. Even if the gradients of the terms are small, the total gradient resists vanishing due to the added term .
Variants of residual blocks
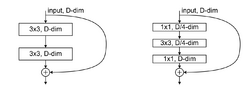
Basic block
A basic block is the simplest building block studied in the original ResNet.[1] This block consists of two sequential 3x3 convolutional layers and a residual connection. The input and output dimensions of both layers are equal.

Bottleneck block
A bottleneck block[1] consists of three sequential convolutional layers and a residual connection. The first layer in this block is a 1×1 convolution for dimension reduction (e.g., to 1/2 of the input dimension); the second layer performs a 3×3 convolution; the last layer is another 1×1 convolution for dimension restoration. The models of ResNet-50, ResNet-101, and ResNet-152 are all based on bottleneck blocks.[1]
Pre-activation block
The pre-activation residual block[6] applies activation functions before applying the residual function . Formally, the computation of a pre-activation residual block can be written as:
where can be any activation (e.g. ReLU) or normalization (e.g. LayerNorm) operation. This design reduces the number of non-identity mappings between residual blocks, and allows an identity mapping directly from the input to the output. This design was used to train models with 200 to over 1000 layers, and was found to consistently outperform variants where the residual path is not an identity function. The pre-activation ResNet with 200 layers took 3 weeks to train for ImageNet on 8 GPUs in 2016.[6]
Since GPT-2, transformer blocks have been mostly implemented as pre-activation blocks. This is often referred to as "pre-normalization" in the literature of transformer models.[7]

Applications
Originally, ResNet was designed for computer vision.[1][8][9]

All transformer architectures include residual connections. Indeed, very deep transformers cannot be trained without them.[10]
The original ResNet paper made no claim on being inspired by biological systems. However, later research has related ResNet to biologically-plausible algorithms.[11][12]
A study published in Science in 2023[13] disclosed the complete connectome of an insect brain (specifically that of a fruit fly larva). This study discovered "multilayer shortcuts" that resemble the skip connections in artificial neural networks, including ResNets.
History
Previous work
Residual connections were noticed in neuroanatomy, such as Lorente de No (1938).[14]Template:Pg McCulloch and Pitts (1943) proposed artificial neural networks and considered those with residual connections.[15]Template:Pg
In 1961, Frank Rosenblatt described a three-layer multilayer perceptron (MLP) model with skip connections.[16]Template:Pg The model was referred to as a "cross-coupled system", and the skip connections were forms of cross-coupled connections.
During the late 1980s, "skip-layer" connections were sometimes used in neural networks. Examples include:[17][18] Lang and Witbrock (1988)[19] trained a fully connected feedforward network where each layer skip-connects to all subsequent layers, like the later DenseNet (2016). In this work, the residual connection was the form
,where
is a randomly-initialized projection connection. They termed it a "short-cut connection". An early neural language model used residual connections and named them "direct connections".[20]

Degradation problem
Sepp Hochreiter discovered the vanishing gradient problem in 1991[21] and argued that it explained why the then-prevalent forms of recurrent neural networks did not work for long sequences. He and Schmidhuber later designed the LSTM architecture to solve this problem,[4][22] which has a "cell state" that can function as a generalized residual connection. The highway network (2015)[23][24] applied the idea of an LSTM unfolded in time to feedforward neural networks, resulting in the highway network. ResNet is equivalent to an open-gated highway network.
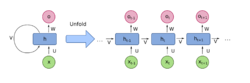
During the early days of deep learning, there were attempts to train increasingly deep models. Notable examples included the AlexNet (2012), which had 8 layers, and the VGG-19 (2014), which had 19 layers.[25] However, stacking too many layers led to a steep reduction in training accuracy,[26] known as the "degradation" problem.[1] In theory, adding additional layers to deepen a network should not result in a higher training loss, but this is what happened with VGGNet.[1] If the extra layers can be set as identity mappings, however, then the deeper network would represent the same function as its shallower counterpart. There is some evidence that the optimizer is not able to approach identity mappings for the parameterized layers, and the benefit of residual connections was to allow identity mappings by default.[6]
In 2014, the state of the art was training deep neural networks with 20 to 30 layers.[25] The research team for ResNet attempted to train deeper ones by empirically testing various methods for training deeper networks, until they came upon the ResNet architecture.[27]
Subsequent work
Wide Residual Network (2016) found that using more channels and fewer layers than the original ResNet improves performance and GPU-computational efficiency, and that a block with two 3×3 convolutions is superior to other configurations of convolution blocks.[28]
DenseNet (2016)[29] connects the output of each layer to the input to each subsequent layer:
Stochastic depth[30] is a regularization method that randomly drops a subset of layers and lets the signal propagate through the identity skip connections. Also known as DropPath, this regularizes training for deep models, such as vision transformers.[31]

ResNeXt (2017) combines the Inception module with ResNet.[32][8]
Squeeze-and-Excitation Networks (2018) added squeeze-and-excitation (SE) modules to ResNet.[33] An SE module is applied after a convolution, and takes a tensor of shape (height, width, channels) as input. Each channel is averaged, resulting in a vector of shape . This is then passed through a multilayer perceptron (with an architecture such as linear-ReLU-linear-sigmoid) before it is multiplied with the original tensor. It won the ILSVRC in 2017.[34]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2016). "Deep Residual Learning for Image Recognition". Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2016.90. https://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf.
- ↑ "ILSVRC2015 Results". https://image-net.org/challenges/LSVRC/2015/results.php.
- ↑ Deng, Jia; Dong, Wei; Socher, Richard; Li, Li-Jia; Li, Kai; Li, Fei-Fei (2009). "ImageNet: A large-scale hierarchical image database". Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2009.5206848.
- ↑ 4.0 4.1 Sepp Hochreiter; Jürgen Schmidhuber (1997). "Long short-term memory". Neural Computation 9 (8): 1735–1780. doi:10.1162/neco.1997.9.8.1735. PMID 9377276. https://www.researchgate.net/publication/13853244.
- ↑ Hanin, Boris; Rolnick, David (2018). "How to Start Training: The Effect of Initialization and Architecture". Conference on Neural Information Processing Systems. 31. Curran Associates, Inc.. https://proceedings.neurips.cc/paper/2018/hash/d81f9c1be2e08964bf9f24b15f0e4900-Paper.pdf.
- ↑ 6.0 6.1 6.2 6.3 6.4 He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2016). "Identity Mappings in Deep Residual Networks". European Conference on Computer Vision. doi:10.1007/978-3-319-46493-0_38. https://link.springer.com/content/pdf/10.1007/978-3-319-46493-0_38.pdf.
- ↑ Radford, Alec; Wu, Jeffrey; Child, Rewon; Luan, David; Amodei, Dario; Sutskever, Ilya (14 February 2019). "Language models are unsupervised multitask learners". https://cdn.openai.com/better-language-models/language_models_are_unsupervised_multitask_learners.pdf.
- ↑ 8.0 8.1 8.2 Zhang, Aston; Lipton, Zachary; Li, Mu; Smola, Alexander J. (2024). "8.6. Residual Networks (ResNet) and ResNeXt". Dive into deep learning. Cambridge New York Port Melbourne New Delhi Singapore: Cambridge University Press. ISBN 978-1-009-38943-3. https://d2l.ai/chapter_convolutional-modern/resnet.html.
- ↑ Szegedy, Christian; Ioffe, Sergey; Vanhoucke, Vincent; Alemi, Alex (2017). "Inception-v4, Inception-ResNet and the impact of residual connections on learning". AAAI Conference on Artificial Intelligence. doi:10.1609/aaai.v31i1.11231. https://cdn.aaai.org/ojs/11231/11231-13-14759-1-2-20201228.pdf.
- ↑ Dong, Yihe; Cordonnier, Jean-Baptiste; Loukas, Andreas (2021). "Attention is not all you need: pure attention loses rank doubly exponentially with depth". International Conference on Machine Learning. PMLR. pp. 2793–2803. http://proceedings.mlr.press/v139/dong21a/dong21a.pdf.
- ↑ Liao, Qianli; Poggio, Tomaso (2016). "Bridging the Gaps Between Residual Learning, Recurrent Neural Networks and Visual Cortex". arXiv:1604.03640 [cs.LG].
- ↑ Xiao, Will; Chen, Honglin; Liao, Qianli; Poggio, Tomaso (2019). "Biologically-Plausible Learning Algorithms Can Scale to Large Datasets". International Conference on Learning Representations.
- ↑ Winding, Michael; Pedigo, Benjamin; Barnes, Christopher; Patsolic, Heather; Park, Youngser; Kazimiers, Tom; Fushiki, Akira; Andrade, Ingrid et al. (10 Mar 2023). "The connectome of an insect brain". Science 379 (6636). doi:10.1126/science.add9330. PMID 36893230.
- ↑ De N, Rafael Lorente (1938-05-01). "Analysis of the Activity of the Chains of Internuncial Neurons" (in en). Journal of Neurophysiology 1 (3): 207–244. doi:10.1152/jn.1938.1.3.207. ISSN 0022-3077. https://www.physiology.org/doi/10.1152/jn.1938.1.3.207.
- ↑ McCulloch, Warren S.; Pitts, Walter (1943-12-01). "A logical calculus of the ideas immanent in nervous activity" (in en). The Bulletin of Mathematical Biophysics 5 (4): 115–133. doi:10.1007/BF02478259. ISSN 1522-9602. https://link.springer.com/article/10.1007/BF02478259.
- ↑ Rosenblatt, Frank (1961). Principles of neurodynamics. perceptrons and the theory of brain mechanisms. https://safari.ethz.ch/digitaltechnik/spring2018/lib/exe/fetch.php?media=neurodynamics1962rosenblatt.pdf#page=327.
- ↑ Rumelhart, David E., Geoffrey E. Hinton, and Ronald J. Williams. "Learning internal representations by error propagation", Parallel Distributed Processing. Vol. 1. 1986.
- ↑ Venables, W. N.; Ripley, Brain D. (1994). Modern Applied Statistics with S-Plus. Springer. pp. 261–262. ISBN 978-3-540-94350-1. https://books.google.com/books?id=ayDvAAAAMAAJ.
- ↑ Lang, Kevin; Witbrock, Michael (1988). "Learning to tell two spirals apart". Proceedings of the 1988 Connectionist Models Summer School: 52–59. https://gwern.net/doc/ai/nn/fully-connected/1988-lang.pdf.
- ↑ Bengio, Yoshua; Ducharme, Réjean; Vincent, Pascal; Jauvin, Christian (2003). "A Neural Probabilistic Language Model". Journal of Machine Learning Research 3 (Feb): 1137–1155. ISSN 1533-7928. https://www.jmlr.org/papers/v3/bengio03a.html.
- ↑ Hochreiter, Sepp (1991). Untersuchungen zu dynamischen neuronalen Netzen (PDF) (diploma thesis). Technical University Munich, Institute of Computer Science, advisor: J. Schmidhuber.
- ↑ Felix A. Gers; Jürgen Schmidhuber; Fred Cummins (2000). "Learning to Forget: Continual Prediction with LSTM". Neural Computation 12 (10): 2451–2471. doi:10.1162/089976600300015015. PMID 11032042.
- ↑ Srivastava, Rupesh Kumar; Greff, Klaus; Schmidhuber, Jürgen (3 May 2015). "Highway Networks". arXiv:1505.00387 [cs.LG].
- ↑ Srivastava, Rupesh Kumar; Greff, Klaus; Schmidhuber, Jürgen (2015). "Training Very Deep Networks". Conference on Neural Information Processing Systems. https://proceedings.neurips.cc/paper/2015/file/215a71a12769b056c3c32e7299f1c5ed-Paper.pdf.
- ↑ 25.0 25.1 Simonyan, Karen; Zisserman, Andrew (2015-04-10). "Very Deep Convolutional Networks for Large-Scale Image Recognition". arXiv:1409.1556 [cs.CV].
- ↑ He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015). "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification". International Conference on Computer Vision. doi:10.1109/ICCV.2015.123. https://openaccess.thecvf.com/content_iccv_2015/papers/He_Delving_Deep_into_ICCV_2015_paper.pdf.
- ↑ Linn, Allison (2015-12-10). "Microsoft researchers win ImageNet computer vision challenge" (in en-US). https://blogs.microsoft.com/ai/microsoft-researchers-win-imagenet-computer-vision-challenge/.
- ↑ Zagoruyko, Sergey; Komodakis, Nikos (2016-05-23). "Wide Residual Networks". arXiv:1605.07146 [cs.CV].
- ↑ Huang, Gao; Liu, Zhuang; van der Maaten, Laurens; Weinberger, Kilian (2017). "Densely Connected Convolutional Networks". Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2017.243. https://openaccess.thecvf.com/content_cvpr_2017/papers/Huang_Densely_Connected_Convolutional_CVPR_2017_paper.pdf.
- ↑ Huang, Gao; Sun, Yu; Liu, Zhuang; Weinberger, Kilian (2016). "Deep Networks with Stochastic Depth". European Conference on Computer Vision. doi:10.1007/978-3-319-46493-0_39. https://link.springer.com/content/pdf/10.1007/978-3-319-46493-0_39.pdf.
- ↑ Lee, Youngwan; Kim, Jonghee; Willette, Jeffrey; Hwang, Sung Ju (2022). "MPViT: Multi-Path Vision Transformer for Dense Prediction" (in en). Conference on Computer Vision and Pattern Recognition. pp. 7287–7296. doi:10.1109/CVPR52688.2022.00714. https://openaccess.thecvf.com/content/CVPR2022/papers/Lee_MPViT_Multi-Path_Vision_Transformer_for_Dense_Prediction_CVPR_2022_paper.pdf.
- ↑ Xie, Saining; Girshick, Ross; Dollar, Piotr; Tu, Zhuowen; He, Kaiming (2017). "Aggregated Residual Transformations for Deep Neural Networks". Conference on Computer Vision and Pattern Recognition. pp. 1492–1500. doi:10.1109/CVPR.2017.634. https://openaccess.thecvf.com/content_cvpr_2017/papers/Xie_Aggregated_Residual_Transformations_CVPR_2017_paper.pdf.
- ↑ Hu, Jie; Shen, Li; Sun, Gang (2018). "Squeeze-and-Excitation Networks". Conference on Computer Vision and Pattern Recognition. pp. 7132–7141. doi:10.1109/CVPR.2018.00745. https://openaccess.thecvf.com/content_cvpr_2018/papers/Hu_Squeeze-and-Excitation_Networks_CVPR_2018_paper.pdf.
- ↑ Jie, Hu (2017). "Squeeze-and-Excitation Networks". Beyond ImageNet Large Scale Visual Recognition Challenge, Workshop at CVPR 2017. https://image-net.org/static_files/files/SENet.pdf.
Template:Artificial intelligence navbox
 |
