Vanishing gradient problem

From HandWiki
Short description: Machine learning model training problem
Machine learning and
data mining
Kernel Machine.svg
Problems
Supervised learning
(classification • regression)
Clustering
Dimensionality reduction
Structured prediction
Anomaly detection
Artificial neural networks
Reinforcement learning
Theory
Machine-learning venues
Glossary of artificial intelligence
Related articles

In machine learning, the vanishing gradient problem is encountered when training recurrent neural networks with gradient-based learning methods and backpropagation. In such methods, during each iteration of training each of the neural networks weights receives an update proportional to the partial derivative of the error function with respect to the current weight.[1] The problem is that as the sequence length increases, the gradient magnitude typically is expected to decrease (or grow uncontrollably), slowing the training process.[1] In the worst case, this may completely stop the neural network from further training.[1] As one example of the problem cause, traditional activation functions such as the hyperbolic tangent function have gradients in the range [-1,1], and backpropagation computes gradients by the chain rule. This has the effect of multiplying n of these small numbers to compute gradients of the early layers in an n-layer network, meaning that the gradient (error signal) decreases exponentially with n while the early layers train very slowly.

Back-propagation allowed researchers to train supervised deep artificial neural networks from scratch, initially with little success. Hochreiter's diplom thesis of 1991 formally identified the reason for this failure in the "vanishing gradient problem",[2][3] which not only affects many-layered feedforward networks,[4] but also recurrent networks.[5] The latter are trained by unfolding them into very deep feedforward networks, where a new layer is created for each time step of an input sequence processed by the network. (The combination of unfolding and backpropagation is termed backpropagation through time.)

When activation functions are used whose derivatives can take on larger values, one risks encountering the related exploding gradient problem.

Prototypical models

This section is based on the paper On the difficulty of training Recurrent Neural Networks by Pascanu, Mikolov, and Bengio.[5]

Recurrent network model

A generic recurrent network has hidden states [math]\displaystyle{ h_1, h_2, ... }[/math] inputs [math]\displaystyle{ u_1, u_2, ... }[/math], and outputs [math]\displaystyle{ x_1, x_2, ... }[/math]. Let it be parametrized by [math]\displaystyle{ \theta }[/math], so that the system evolves as[math]\displaystyle{ (h_t, x_t) = F(h_{t-1}, u_t, \theta) }[/math]Often, the output [math]\displaystyle{ x_t }[/math] is a function of [math]\displaystyle{ h_t }[/math], as some [math]\displaystyle{ x_t = G(h_t) }[/math]. The vanishing gradient problem already presents itself clearly when [math]\displaystyle{ x_t = h_t }[/math], so we simplify our notation to the special case with:[math]\displaystyle{ x_t = F(x_{t-1}, u_t, \theta) }[/math] Now, take its differential:[math]\displaystyle{ \begin{align} dx_t &= \nabla_\theta F(x_{t-1}, u_t, \theta) d\theta + \nabla_x F(x_{t-1}, u_t, \theta) dx_{t-1} \\ &= \nabla_\theta F(x_{t-1}, u_t, \theta) d\theta + \nabla_x F(x_{t-1}, u_t, \theta)(\nabla_\theta F(x_{t-2}, u_{t-1}, \theta) d\theta + \nabla_x F(x_{t-2}, u_{t-1}, \theta) dx_{t-2}) \\ &= \cdots \\ &= \left(\nabla_\theta F(x_{t-1}, u_t, \theta) + \nabla_x F(x_{t-1}, u_t, \theta) \nabla_\theta F(x_{t-2}, u_{t-1}, \theta) + \cdots \right) d\theta \end{align} }[/math]Training the network requires us to define a loss function to be minimized. Let it be [math]\displaystyle{ L(x_T, u_1, ..., u_T) }[/math][note 1], then minimizing it by gradient descent gives

[math]\displaystyle{ dL = \nabla_x L(x_T, u_1, ..., u_T)\left(\nabla_\theta F(x_{t-1}, u_t, \theta) + \nabla_x F(x_{t-1}, u_t, \theta) \nabla_\theta F(x_{t-2}, u_{t-1}, \theta) + \cdots \right) d\theta }[/math]

 

 

 

 

(loss differential)

[math]\displaystyle{ \Delta \theta = -\eta \cdot\left[ \nabla_x L(x_T)\left(\nabla_\theta F(x_{t-1}, u_t, \theta) + \nabla_x F(x_{t-1}, u_t, \theta) \nabla_\theta F(x_{t-2}, u_{t-1}, \theta) + \cdots \right) \right]^T }[/math]where [math]\displaystyle{ \eta }[/math] is the learning rate.

The vanishing/exploding gradient problem appears because there are repeated multiplications, of the form[math]\displaystyle{ \nabla_x F(x_{t-1}, u_t, \theta) \nabla_x F(x_{t-2}, u_{t-1}, \theta)\nabla_x F(x_{t-3}, u_{t-2}, \theta) \cdots }[/math]

Example: recurrent network with sigmoid activation

For a concrete example, consider a typical recurrent network defined by

[math]\displaystyle{ x_t = F(x_{t-1}, u_t, \theta) = W_{rec} \sigma(x_{t-1}) + W_{in} u_t + b }[/math]where [math]\displaystyle{ \theta = (W_{rec}, W_{in}) }[/math] is the network parameter, [math]\displaystyle{ \sigma }[/math] is the sigmoid activation function[note 2], applied to each vector coordinate separately, and [math]\displaystyle{ b }[/math] is the bias vector.

Then, [math]\displaystyle{ \nabla_x F(x_{t-1}, u_t, \theta) = W_{rec} \mathop{diag}(\sigma'(x_{t-1})) }[/math], and so [math]\displaystyle{ \begin{align} \nabla_x F(x_{t-1}, u_t, \theta) & \nabla_x F(x_{t-2}, u_{t-1}, \theta)\cdots \nabla_x F(x_{t-k}, u_{t-k+1}, \theta) \\ = W_{rec} \mathop{diag}(\sigma'(x_{t-1})) & W_{rec} \mathop{diag}(\sigma'(x_{t-2})) \cdots W_{rec} \mathop{diag}(\sigma'(x_{t-k})) \end{align} }[/math]Since [math]\displaystyle{ |\sigma'|\leq 1 }[/math], the operator norm of the above multiplication is bounded above by [math]\displaystyle{ \|W_{rec}\|^k }[/math]. So if the spectral radius of [math]\displaystyle{ W_{rec} }[/math] is [math]\displaystyle{ \gamma\lt 1 }[/math], then at large [math]\displaystyle{ k }[/math], the above multiplication has operator norm bounded above by [math]\displaystyle{ \gamma^k \to 0 }[/math]. This is the prototypical vanishing gradient problem.

The effect of a vanishing gradient is that the network cannot learn long-range effects. Recall Equation (loss differential):[math]\displaystyle{ \nabla_\theta L = \nabla_x L(x_T, u_1, ..., u_T)\left(\nabla_\theta F(x_{t-1}, u_t, \theta) + \nabla_x F(x_{t-1}, u_t, \theta) \nabla_\theta F(x_{t-2}, u_{t-1}, \theta) + \cdots \right) }[/math]The components of [math]\displaystyle{ \nabla_\theta F(x, u, \theta) }[/math] are just components of [math]\displaystyle{ \sigma(x) }[/math] and [math]\displaystyle{ u }[/math], so if [math]\displaystyle{ u_t, u_{t-1}, ... }[/math] are bounded, then [math]\displaystyle{ \|\nabla _{\theta }F(x_{t-k-1},u_{t-k},\theta)\| }[/math] is also bounded by some [math]\displaystyle{ M\gt 0 }[/math], and so the terms in [math]\displaystyle{ \nabla_\theta L }[/math] decay as [math]\displaystyle{ M\gamma^k }[/math]. This means that, effectively, [math]\displaystyle{ \nabla_\theta L }[/math] is affected only by the first [math]\displaystyle{ O(\gamma^{-1}) }[/math] terms in the sum.

If [math]\displaystyle{ \gamma\geq 1 }[/math], the above analysis does not quite work.[note 3] For the prototypical exploding gradient problem, the next model is clearer.

Dynamical systems model

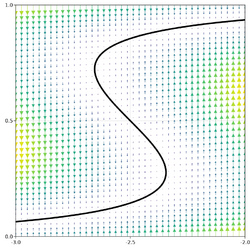
Bifurcation diagram of the one-neuron recurrent network. Horizontal axis is b, and vertical axis is x. The black curve is the set of stable and unstable equilibria. Notice that the system exhibits hysteresis, and can be used as a one-bit memory.

Following (Doya, 1993),[6] consider this one-neuron recurrent network with sigmoid activation:[math]\displaystyle{ x_{t+1} = (1-\epsilon) x_t + \epsilon \sigma(wx_t + b) + \epsilon w' u_t }[/math]At the small [math]\displaystyle{ \epsilon }[/math] limit, the dynamics of the network becomes[math]\displaystyle{ \frac{dx}{dt} = -x(t) + \sigma(wx(t)+b) + w' u(t) }[/math]Consider first the autonomous case, with [math]\displaystyle{ u=0 }[/math]. Set [math]\displaystyle{ w=5.0 }[/math], and vary [math]\displaystyle{ b }[/math] in [math]\displaystyle{ [-3, -2] }[/math]. As [math]\displaystyle{ b }[/math] decreases, the system has 1 stable point, then has 2 stable points and 1 unstable point, and finally has 1 stable point again. Explicitly, the stable points are [math]\displaystyle{ (x, b) = \left(x, \ln\left(\frac{x}{1-x}\right)-5x \right) }[/math].

Now consider [math]\displaystyle{ \frac{\Delta x(T)}{\Delta x(0)} }[/math] and [math]\displaystyle{ \frac{\Delta x(T)}{\Delta b} }[/math], where [math]\displaystyle{ T }[/math] is large enough that the system has settled into one of the stable points.

If [math]\displaystyle{ (x(0), b) }[/math] puts the system very close to an unstable point, then a tiny variation in [math]\displaystyle{ x(0) }[/math] or [math]\displaystyle{ b }[/math] would make [math]\displaystyle{ x(T) }[/math] move from one stable point to the other. This makes [math]\displaystyle{ \frac{\Delta x(T)}{\Delta x(0)} }[/math] and [math]\displaystyle{ \frac{\Delta x(T)}{\Delta b} }[/math] both very large, a case of the exploding gradient.

If [math]\displaystyle{ (x(0), b) }[/math] puts the system far from an unstable point, then a small variation in [math]\displaystyle{ x(0) }[/math] would have no effect on [math]\displaystyle{ x(T) }[/math], making [math]\displaystyle{ \frac{\Delta x(T)}{\Delta x(0)}= 0 }[/math], a case of the vanishing gradient.

Note that in this case, [math]\displaystyle{ \frac{\Delta x(T)}{\Delta b}\approx \frac{\partial x(T)}{\partial b} = \left(\frac{1}{x(T)(1-x(T))}-5\right)^{-1} }[/math] neither decays to zero nor blows up to infinity. Indeed, it's the only well-behaved gradient, which explains why early researches focused on learning or designing recurrent networks systems that could perform long-ranged computations (such as outputting the first input it sees at the very end of an episode) by shaping its stable attractors.[7]

For the general case, the intuition still holds ([5] Figures 3, 4, and 5).

Geometric model

Continue using the above one-neuron network, fixing [math]\displaystyle{ w = 5, x(0) = 0.5, u(t) = 0 }[/math], and consider a loss function defined by [math]\displaystyle{ L(x(T)) = (0.855 - x(T))^2 }[/math]. This produces a rather pathological loss landscape: as [math]\displaystyle{ b }[/math] approach [math]\displaystyle{ -2.5 }[/math] from above, the loss approaches zero, but as soon as [math]\displaystyle{ b }[/math] crosses [math]\displaystyle{ -2.5 }[/math], the attractor basin changes, and loss jumps to 0.50.[note 4]

Consequently, attempting to train [math]\displaystyle{ b }[/math] by gradient descent would "hit a wall in the loss landscape", and cause exploding gradient. A slightly more complex situation is plotted in,[5] Figures 6.

Solutions

To overcome this problem, several methods were proposed.

Batch normalization

Batch normalization is a standard method for solving both the exploding and the vanishing gradient problems.[8][9]

Multi-level hierarchy

One is Jürgen Schmidhuber's multi-level hierarchy of networks (1992) pre-trained one level at a time through unsupervised learning, fine-tuned through backpropagation.[10] Here each level learns a compressed representation of the observations that is fed to the next level.

Related approach

Similar ideas have been used in feed-forward neural networks for unsupervised pre-training to structure a neural network, making it first learn generally useful feature detectors. Then the network is trained further by supervised backpropagation to classify labeled data. The deep belief network model by Hinton et al. (2006) involves learning the distribution of a high level representation using successive layers of binary or real-valued latent variables. It uses a restricted Boltzmann machine to model each new layer of higher level features. Each new layer guarantees an increase on the lower-bound of the log likelihood of the data, thus improving the model, if trained properly. Once sufficiently many layers have been learned the deep architecture may be used as a generative model by reproducing the data when sampling down the model (an "ancestral pass") from the top level feature activations.[11] Hinton reports that his models are effective feature extractors over high-dimensional, structured data.[12]

Long short-term memory

Main page: Long short-term memory

Another technique particularly used for recurrent neural networks is the long short-term memory (LSTM) network of 1997 by Hochreiter & Schmidhuber.[13] In 2009, deep multidimensional LSTM networks demonstrated the power of deep learning with many nonlinear layers, by winning three ICDAR 2009 competitions in connected handwriting recognition, without any prior knowledge about the three different languages to be learned.[14][15]

Faster hardware

Hardware advances have meant that from 1991 to 2015, computer power (especially as delivered by GPUs) has increased around a million-fold, making standard backpropagation feasible for networks several layers deeper than when the vanishing gradient problem was recognized. Schmidhuber notes that this "is basically what is winning many of the image recognition competitions now", but that it "does not really overcome the problem in a fundamental way"[16] since the original models tackling the vanishing gradient problem by Hinton and others were trained in a Xeon processor, not GPUs.[11]

Residual networks

One of the newest and most effective ways to resolve the vanishing gradient problem is with residual neural networks,[17] or ResNets (not to be confused with recurrent neural networks). ResNets refer to neural networks where skip connections or residual connections are part of the network architecture. These skip connections allow gradient information to pass through the layers, by creating "highways" of information, where the output of a previous layer/activation is added to the output of a deeper layer. This allows information from the earlier parts of the network to be passed to the deeper parts of the network, helping maintain signal propagation even in deeper networks. Skip connections are a critical component of what allowed successful training of deeper neural networks.

ResNets yielded lower training error (and test error) than their shallower counterparts simply by reintroducing outputs from shallower layers in the network to compensate for the vanishing data.[17] Note that ResNets are an ensemble of relatively shallow nets and do not resolve the vanishing gradient problem by preserving gradient flow throughout the entire depth of the network – rather, they avoid the problem simply by constructing ensembles of many short networks together. (Ensemble by Construction[18])

Other activation functions

Rectifiers such as ReLU suffer less from the vanishing gradient problem, because they only saturate in one direction.[19]

Weight initialization

Weight initialization is another approach that has been proposed to reduce the vanishing gradient problem in deep networks.

Kumar suggested that the distribution of initial weights should vary according to activation function used and proposed to initialize the weights in networks with the logistic activation function using a Gaussian distribution with a zero mean and a standard deviation of 3.6/sqrt(N), where N is the number of neurons in a layer.[20]

Recently, Yilmaz and Poli[21] performed a theoretical analysis on how gradients are affected by the mean of the initial weights in deep neural networks using the logistic activation function and found that gradients do not vanish if the mean of the initial weights is set according to the formula: max(−1,-8/N). This simple strategy allows networks with 10 or 15 hidden layers to be trained very efficiently and effectively using the standard backpropagation.

Other

Behnke relied only on the sign of the gradient (Rprop) when training his Neural Abstraction Pyramid[22] to solve problems like image reconstruction and face localization.[citation needed]

Neural networks can also be optimized by using a universal search algorithm on the space of neural network's weights, e.g., random guess or more systematically genetic algorithm. This approach is not based on gradient and avoids the vanishing gradient problem.[23]

See also

Notes

  1. ↑ A more general loss function could depend on the entire sequence of outputs, as [math]\displaystyle{ L(x_{1},...,x_{T}, u_1, ..., u_T)=\sum _{t=1}^{T}{\mathcal {E}}(x_{t}, u_1, ..., u_t) }[/math] for which the problem is the same, just with more complex notations.
  2. ↑ Any activation function works, as long as it is differentiable with bounded derivative.
  3. ↑ Consider [math]\displaystyle{ W_{rec} = \begin{bmatrix} 0 & 2\\ \epsilon & 0 \end{bmatrix} }[/math] and [math]\displaystyle{ D = \begin{bmatrix} c & 0\\ 0 & c \end{bmatrix} }[/math], with [math]\displaystyle{ \epsilon \gt \frac 1 2 }[/math] and [math]\displaystyle{ c\in (0, 1) }[/math]. Then [math]\displaystyle{ W_{rec} }[/math] has spectral radius [math]\displaystyle{ \sqrt{2\epsilon}\gt 1 }[/math], and [math]\displaystyle{ (W_{rec}D)^{2N} = (2\epsilon \cdot c^2)^N I_{2\times 2} }[/math], which might go to infinity or zero depending on choice of [math]\displaystyle{ c }[/math].
  4. ↑ This is because at [math]\displaystyle{ b = -2.5 }[/math], the two stable attractors are [math]\displaystyle{ x=0.145, 0.855 }[/math], and the unstable attractor is [math]\displaystyle{ x=0.5 }[/math].

References

  1. ↑ 1.0 1.1 1.2 Basodi, Sunitha; Ji, Chunyan; Zhang, Haiping; Pan, Yi (September 2020). "Gradient amplification: An efficient way to train deep neural networks". Big Data Mining and Analytics 3 (3): 198. doi:10.26599/BDMA.2020.9020004. ISSN 2096-0654. 
  2. ↑ Hochreiter, S. (1991). Untersuchungen zu dynamischen neuronalen Netzen (PDF) (Diplom thesis). Institut f. Informatik, Technische Univ. Munich.
  3. ↑ Hochreiter, S.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. (2001). "Gradient flow in recurrent nets: the difficulty of learning long-term dependencies". in Kremer, S. C.; Kolen, J. F.. A Field Guide to Dynamical Recurrent Neural Networks. IEEE Press. ISBN 0-7803-5369-2. 
  4. ↑ Goh, Garrett B.; Hodas, Nathan O.; Vishnu, Abhinav (2017-06-15). "Deep learning for computational chemistry" (in en). Journal of Computational Chemistry 38 (16): 1291–1307. doi:10.1002/jcc.24764. PMID 28272810. Bibcode: 2017arXiv170104503G. 
  5. ↑ 5.0 5.1 5.2 5.3 Pascanu, Razvan; Mikolov, Tomas; Bengio, Yoshua (2012-11-21). "On the difficulty of training Recurrent Neural Networks". arXiv:1211.5063 [cs.LG].
  6. ↑ Doya, K. (1992). "Bifurcations in the learning of recurrent neural networks". [Proceedings] 1992 IEEE International Symposium on Circuits and Systems. 6. IEEE. pp. 2777–2780. doi:10.1109/iscas.1992.230622. ISBN 0-7803-0593-0. http://dx.doi.org/10.1109/iscas.1992.230622. 
  7. ↑ Bengio, Y.; Simard, P.; Frasconi, P. (March 1994). "Learning long-term dependencies with gradient descent is difficult". IEEE Transactions on Neural Networks 5 (2): 157–166. doi:10.1109/72.279181. ISSN 1941-0093. PMID 18267787. https://ieeexplore.ieee.org/document/279181/;jsessionid=SMWnZdZeKnZotfiKpw4WmPN3aVjDWTzXEGlc8wIe2ZPryNFwofRz!1804793449. 
  8. ↑ Ioffe, Sergey; Szegedy, Christian (2015-06-01). "Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift" (in en). International Conference on Machine Learning (PMLR): 448–456. https://proceedings.mlr.press/v37/ioffe15.html. 
  9. ↑ Santurkar, Shibani; Tsipras, Dimitris; Ilyas, Andrew; Madry, Aleksander (2018). "How Does Batch Normalization Help Optimization?". Advances in Neural Information Processing Systems (Curran Associates, Inc.) 31. https://proceedings.neurips.cc/paper/2018/hash/905056c1ac1dad141560467e0a99e1cf-Abstract.html. 
  10. ↑ J. Schmidhuber., "Learning complex, extended sequences using the principle of history compression," Neural Computation, 4, pp. 234–242, 1992.
  11. ↑ 11.0 11.1 Hinton, G. E.; Osindero, S.; Teh, Y. (2006). "A fast learning algorithm for deep belief nets". Neural Computation 18 (7): 1527–1554. doi:10.1162/neco.2006.18.7.1527. PMID 16764513. http://www.cs.toronto.edu/~hinton/absps/fastnc.pdf. 
  12. ↑ Hinton, G. (2009). "Deep belief networks". Scholarpedia 4 (5): 5947. doi:10.4249/scholarpedia.5947. Bibcode: 2009SchpJ...4.5947H. 
  13. ↑ Hochreiter, Sepp; Schmidhuber, Jürgen (1997). "Long Short-Term Memory". Neural Computation 9 (8): 1735–1780. doi:10.1162/neco.1997.9.8.1735. PMID 9377276. 
  14. ↑ Graves, Alex; and Schmidhuber, Jürgen; Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks, in Bengio, Yoshua; Schuurmans, Dale; Lafferty, John; Williams, Chris K. I.; and Culotta, Aron (eds.), Advances in Neural Information Processing Systems 22 (NIPS'22), December 7th–10th, 2009, Vancouver, BC, Neural Information Processing Systems (NIPS) Foundation, 2009, pp. 545–552
  15. ↑ Graves, A.; Liwicki, M.; Fernandez, S.; Bertolami, R.; Bunke, H.; Schmidhuber, J. (2009). "A Novel Connectionist System for Improved Unconstrained Handwriting Recognition". IEEE Transactions on Pattern Analysis and Machine Intelligence 31 (5): 855–868. doi:10.1109/tpami.2008.137. PMID 19299860. 
  16. ↑ Schmidhuber, Jürgen (2015). "Deep learning in neural networks: An overview". Neural Networks 61: 85–117. doi:10.1016/j.neunet.2014.09.003. PMID 25462637. 
  17. ↑ 17.0 17.1 He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2016). "Deep Residual Learning for Image Recognition". Las Vegas, NV, USA: IEEE. 770–778. doi:10.1109/CVPR.2016.90. ISBN 978-1-4673-8851-1. https://ieeexplore.ieee.org/document/7780459. 
  18. ↑ Veit, Andreas; Wilber, Michael; Belongie, Serge (2016-05-20). "Residual Networks Behave Like Ensembles of Relatively Shallow Networks". arXiv:1605.06431 [cs.CV].
  19. ↑ Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011-06-14). "Deep Sparse Rectifier Neural Networks" (in en). PMLR: 315–323. http://proceedings.mlr.press/v15/glorot11a.html. 
  20. ↑ Kumar, Siddharth Krishna. "On weight initialization in deep neural networks." arXiv preprint arXiv:1704.08863 (2017).
  21. ↑ Yilmaz, Ahmet; Poli, Riccardo (2022-09-01). "Successfully and efficiently training deep multi-layer perceptrons with logistic activation function simply requires initializing the weights with an appropriate negative mean" (in en). Neural Networks 153: 87–103. doi:10.1016/j.neunet.2022.05.030. ISSN 0893-6080. PMID 35714424. https://www.sciencedirect.com/science/article/pii/S0893608022002040. 
  22. ↑ Sven Behnke (2003). Hierarchical Neural Networks for Image Interpretation.. Lecture Notes in Computer Science. 2766. Springer. http://www.ais.uni-bonn.de/books/LNCS2766.pdf. 
  23. ↑ "Sepp Hochreiter's Fundamental Deep Learning Problem (1991)". http://people.idsia.ch/~juergen/fundamentaldeeplearningproblem.html. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Vanishing_gradient_problem&oldid=3371202"