rg chromaticity

From HandWiki
Short description: Color space

The RGB chromaticity space, two dimensions of the normalized RGB space,[1] is a chromaticity space, a two-dimensional color space in which there is no intensity information.

In the RGB color space a pixel is identified by the intensity of red, green, and blue primary colors. Therefore, a bright red can be represented as (R,G,B) (255,0,0), while a dark red may be (40,0,0). In the normalized RGB space or RG space, a color is represented by the proportion of red, green, and blue in the color, rather than by the intensity of each. Since these proportions must always add up to a total of 1, we are able to quote just the red and green proportions of the color, and can calculate the blue value if necessary.

Conversion between RGB and RG Chromaticity

Given a color (R,G,B) where R, G, B = linear intensity of red, green and blue, this can be converted to color [math]\displaystyle{ (r,g,b) }[/math] where [math]\displaystyle{ r, g, b }[/math] imply the proportion of red, green and blue in the original color:[2] [3]

[math]\displaystyle{ r = \frac{R}{R+G+B} }[/math]

[math]\displaystyle{ g = \frac{G}{R+G+B} }[/math]

[math]\displaystyle{ b = \frac{B}{R+G+B} }[/math]

[math]\displaystyle{ r+g+b = 1 }[/math]

The sum of rgb will always equal one, because of this property the b dimension can be thrown away without causing any loss in information. The reverse conversion is not possible with only two dimensions, as the intensity information is lost during the conversion to rg chromaticity, e.g. (1/3, 1/3, 1/3) has equal proportions of each color, but it is not possible to determine whether this corresponds to black, gray, or white. If R, G, B, is normalized to r, g, G color space the conversion can be computed by the following:

[math]\displaystyle{ R = \frac{rG}{g} }[/math]

[math]\displaystyle{ G = G }[/math]

[math]\displaystyle{ B =\frac{(1-r-g)G}{g} }[/math]

The conversion from rgG to RGB, is the same as the conversion from xyY to XYZ.[4] The conversion requires at least some information relative to the intensity of the scene. For this reason if the G is preserved then the inverse is possible.

Version used in computer vision

Motivation

Computer vision algorithms tend to suffer from varying imaging conditions. To make more robust computer vision algorithms it is important to use a (approximately) color invariant color space. Color invariant color spaces are desensitized to disturbances in the image. One common problem in computer vision is varying light source (color and intensity) between multiple images and within a single image.[5]

The rg colorspace is used out of a desire for pixel-based photometric invariance. For example, if a scene is lit by a spotlight, an object of a given color will change in apparent color as it moves across the scene. Where color is being used to track an object in an RGB image, this can cause problems. Removing the intensity component should keep the color constant.

Practice

In practice, computer vision uses an "incorrect" form of rg colorspace derived directly from gamma-corrected RGB, typically sRGB. As a result, full removal of intensity is not achieved and 3D objects still show some of fringing.

Illustration

A photograph with varying illumination levels.
A visual representation of the chromaticity of the image. Each pixel has been scaled so the total red, green, and blue coordinates sum to 1. Notice the effect on the foliage and shadowed regions.
A visual representation of the average value of red, green, and blue coordinates for each pixel in the original image. This information can be combined with the rg chromaticity information to reconstruct the original image.

rg color space

Normalized rg Color Space

r, g, and b chromaticity coordinates are ratios of the one tristimulus value over the sum of all three tristimulus values. A neutral object infers equal values of red, green and blue stimulus. The lack of luminance information in rg prevents having more than 1 neutral point where all three coordinates are of equal value. The white point of the rg chromaticity diagram is defined by the point (1/3,1/3). The white point has one third red, one third green and the final third blue. On an rg chromaticity diagram the first quadrant where all values of r and g are positive forms a right triangle. With max r equals 1 unit along the x and max g equals 1 unit along the y axis. Connecting a line from the max r (1,0) to max g (0,1) from a straight line with slope of negative 1. Any sample that falls on this line has no blue. Moving along the line from max r to max g, shows a decrease in red and an increase of green in the sample, without blue changing. The further a sample moves from this line the more blue is present in the sample trying to be matched.

CIE RGB

The CIE 1931 RGB Color matching functions. The color matching functions are the amounts of primaries needed to match the monochromatic test primary at the wavelength shown on the horizontal scale.

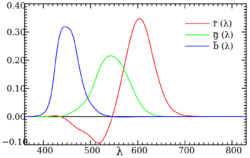
RGB is a color mixture system. Once the color matching function are determined the tristimulus values can be determined easily. Since standardization is required to compare results, CIE established standards to determine color matching function.[6]

  1. The reference stimuli must be monochromatic lights R, G, B. With wavelengths [math]\displaystyle{ \lambda_R=700.0nm, \lambda_G=546.1nm, \lambda_B=435.8nm }[/math] respectively.
  2. The basic stimulus is white with equal energy spectrum. Require a ratio of 1.000:4.5907:0.0601 (RGB) to match white point.

Therefore, a white with equi-energy lights of 1.000 + 4.5907 + 0.0601 = 5.6508 lm can be matched by mixing together R, G and B. Guild and Wright used 17 subjects to determine RGB color matching functions.[7] RGB color matching serve as the base for rg chromaticity. The RGB color matching functions are used to determine the tristimulus RGB values for a spectrum. Normalizing the RGB tristimulus values converts the tristimulus into rgb. Normalized RGB tristimulus value can be plotted on an rg chromaticity diagram.

An example of color matching function below. [math]\displaystyle{ [F_{\lambda}] }[/math] is any monochromatic. Any monochromatic can be matched by adding reference stimuli [math]\displaystyle{ R[R], G[G] }[/math] and [math]\displaystyle{ B[B] }[/math]. The test light is also to bright to account for this reference stimuli is added to the target to dull the saturation. Thus [math]\displaystyle{ R }[/math] is negative. [math]\displaystyle{ [R], [G] }[/math] and [math]\displaystyle{ [B] }[/math] can be defined as a vector in a three-dimensional space. This three-dimensional space is defined as the color space. Any color [math]\displaystyle{ [F] }[/math] can be reached by matching a given amount of [math]\displaystyle{ [R], [G] }[/math] and [math]\displaystyle{ [B] }[/math].

[math]\displaystyle{ [F_{\lambda}]+R[R] =G[G]+B[B] }[/math]

[math]\displaystyle{ [F_{\lambda}]=-R[R]+ G[G]+B[B] }[/math]

The negative[math]\displaystyle{ [R] }[/math] calls for color matching functions that are negative at certain wavelengths. This is evidence of why the [math]\displaystyle{ \overline{r} }[/math] color matching function appears to have negative tristimulus values.

rg chromaticity diagram

rg Chromaticity Diagram

The figure to the side is a plotted rg chromaticity diagram. Noting the importance of the E which is defined as the white point where rg are equal and have a value of 1/3. Next notice the straight line from (0,1) to (1,0), follows the expression y = -x + 1. As the x (red) increases the y (green) decreases by the same amount. Any point on the line represents the limit in rg, and can be defined by a point that has no b information and formed by some combination of r and g. Moving of the linear line towards E represents a decrease in r and g and an increase in b. In computer vision and digital imagery only use the first quadrant because a computer cannot display negative RGB values. The range of RGB is 0-255 for most displays. But when trying to form color matches using real stimuli negative values are needed according to Grassmann's Laws to match all possible colors. This is why the rg chromaticity diagram extends in the negative r direction.

Conversion xyY color system

Avoiding negative color coordinate values prompted the change from to rg to xy. Negative coordinates are used in rg space because when making a spectral sample match can be created by adding stimulus to the sample. The color matching functions r, g, and b are negative at certain wavelengths to allow for any monochromatic sample to be matched. This is why in the rg chromaticity diagram the spectral locus extents into the negative r direction and ever so slightly into the negative g direction. On an xy chromaticity diagram the spectral locus if formed by all positive values of x and y.

See also

References

  1. ↑ J. B. Martinkauppi; M. Pietikäinen (2005). "Facial Skin Color Modeling". Handbook of face recognition. Springer Science & Business. p. 117. ISBN 978-0-387-40595-7. https://books.google.com/books?id=amVDaTdgKYcC&q=%22normalized+RGB%22+rg&pg=PA117. 
  2. ↑ W. T. Wintringham (1951). "Color Television and Colorimetry". in D L. MacAdam. Selected Papers on Colorimetry Fundamentals. SPIE - The International Society for Optical Engineering. p. 343. ISBN 0-8194-1296-1. 
  3. ↑ Fairman, Hugh S; Brill, Michael H; Hemmendinger, Henry (1997). "How the CIE 1931 color-matching functions were derived from Wright-Guild data". Color Research & Application 22: 11–23. doi:10.1002/(SICI)1520-6378(199702)22:1<11::AID-COL4>3.0.CO;2-7. 
  4. ↑ Lindloom, Bruce (13 March 2009). "xyY to XYZ". http://www.brucelindbloom.com/index.html?Eqn_xyY_to_XYZ.html. Retrieved 7 December 2013. 
  5. ↑ T. Gevers; A. Gijsenji; J. van de Weijer; J. Geusebroek (2012). "Pixel-Based Photometric Invariance". in M. A. Kriss. Color in Computer Vision Fundamentals and Applications. Wiley - IS&T Series. p. 50. ISBN 978-0-470-89084-4. 
  6. ↑ N. Ohto; A. R. Robertson (2005). "CIE Standard Colorimetric System". in M. A. Kriss. Colorimetry Fundamentals and Applications. Wiley - IS&T Series. p. 65. ISBN 978-0-470-09472-3. 
  7. ↑ R. W. G. Hunt (2004). "The Colour Triangle". in M. A. Kriss. The Reproduction of Colour. Wiley - IS&T Series. p. 71. ISBN 0-470-02425-9. https://archive.org/details/reproductionofco0000hunt/page/71. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Rg_chromaticity&oldid=3364465"