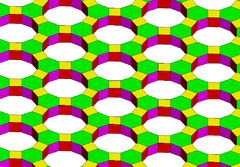
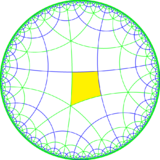
Rhombitetrahexagonal tiling
In geometry, the rhombitetrahexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{6,4}. It can be seen as constructed as a rectified tetrahexagonal tiling, r{6,4}, as well as an expanded order-4 hexagonal tiling or expanded order-6 square tiling.
Constructions
There are two uniform constructions of this tiling, one from [6,4] or (*642) symmetry, and secondly removing the mirror middle, [6,1+,4], gives a rectangular fundamental domain [∞,3,∞], (*3222).
| Name | Rhombitetrahexagonal tiling | |
|---|---|---|
| Image | 
|

|
| Symmetry | [6,4] (*642) |
[6,1+,4] = [∞,3,∞] (*3222) |
| Schläfli symbol | rr{6,4} | t0,1,2,3{∞,3,∞} |
| Coxeter diagram |
There are 3 lower symmetry forms seen by including edge-colorings: ![]()
![]()
![]()
![]()
![]() sees the hexagons as truncated triangles, with two color edges, with [6,4+] (4*3) symmetry.
sees the hexagons as truncated triangles, with two color edges, with [6,4+] (4*3) symmetry. ![]()
![]()
![]()
![]()
![]() sees the yellow squares as rectangles, with two color edges, with [6+,4] (6*2) symmetry. A final quarter symmetry combines these colorings, with [6+,4+] (32×) symmetry, with 2 and 3 fold gyration points and glide reflections.
sees the yellow squares as rectangles, with two color edges, with [6+,4] (6*2) symmetry. A final quarter symmetry combines these colorings, with [6+,4+] (32×) symmetry, with 2 and 3 fold gyration points and glide reflections.
| Lower symmetry constructions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
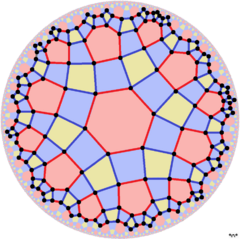 [6,4], (*632) |
 [6,4+], (4*3) | ||||||||||
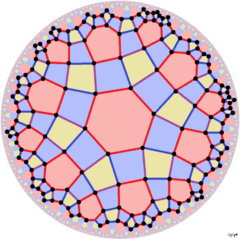 [6+,4], (6*2) |
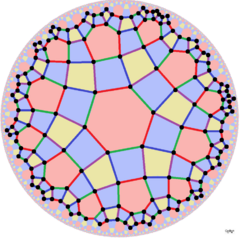 [6+,4+], (32×) | ||||||||||
This four color tiling is related to a semiregular infinite skew polyhedron with the same vertex figure in Euclidean 3-space with a prismatic honeycomb construction of ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Symmetry
The dual tiling, called a deltoidal tetrahexagonal tiling, represents the fundamental domains of the *3222 orbifold, shown here from three different centers. Its fundamental domain is a Lambert quadrilateral, with 3 right angles. This symmetry can be seen from a [6,4], (*642) triangular symmetry with one mirror removed, constructed as [6,1+,4], (*3222). Removing half of the blue mirrors doubles the domain again into *3322 symmetry.
Related polyhedra and tiling
See also
- Square tiling
- Tilings of regular polygons
- List of uniform planar tilings
- List of regular polytopes
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8.
External links
- Weisstein, Eric W.. "Hyperbolic tiling". http://mathworld.wolfram.com/HyperbolicTiling.html.
- Weisstein, Eric W.. "Poincaré hyperbolic disk". http://mathworld.wolfram.com/PoincareHyperbolicDisk.html.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
 |