Rectification (geometry)

Short description: Operation in Euclidean geometry

A rectified cube is a cuboctahedron – edges reduced to vertices, and vertices expanded into new faces

A birectified cube is an octahedron – faces are reduced to points and new faces are centered on the original vertices.

A rectified cubic honeycomb – edges reduced to vertices, and vertices expanded into new cells.

In Euclidean geometry, rectification, also known as critical truncation or complete-truncation, is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope.

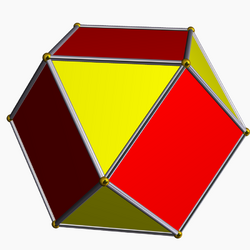
A rectification operator is sometimes denoted by the letter r with a Schläfli symbol. For example, r{4,3} is the rectified cube, also called a cuboctahedron, and also represented as [math]\displaystyle{ \begin{Bmatrix} 4 \\ 3 \end{Bmatrix} }[/math]. And a rectified cuboctahedron rr{4,3} is a rhombicuboctahedron, and also represented as [math]\displaystyle{ r\begin{Bmatrix} 4 \\ 3 \end{Bmatrix} }[/math].

Conway polyhedron notation uses a for ambo as this operator. In graph theory this operation creates a medial graph.

The rectification of any regular self-dual polyhedron or tiling will result in another regular polyhedron or tiling with a tiling order of 4, for example the tetrahedron {3,3} becoming an octahedron {3,4}. As a special case, a square tiling {4,4} will turn into another square tiling {4,4} under a rectification operation.

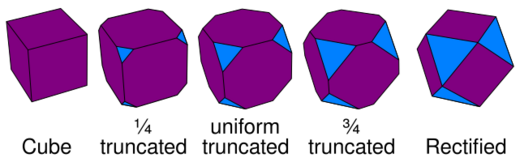
Example of rectification as a final truncation to an edge

Rectification is the final point of a truncation process. For example, on a cube this sequence shows four steps of a continuum of truncations between the regular and rectified form:

Higher degree rectifications

Higher degree rectification can be performed on higher-dimensional regular polytopes. The highest degree of rectification creates the dual polytope. A rectification truncates edges to points. A birectification truncates faces to points. A trirectification truncates cells to points, and so on.

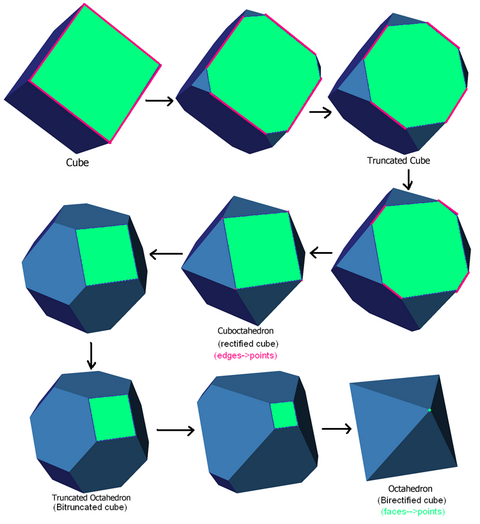
Example of birectification as a final truncation to a face

This sequence shows a birectified cube as the final sequence from a cube to the dual where the original faces are truncated down to a single point:

In polygons

The dual of a polygon is the same as its rectified form. New vertices are placed at the center of the edges of the original polygon.

In polyhedra and plane tilings

Further information: Quasiregular polyhedron

Each platonic solid and its dual have the same rectified polyhedron. (This is not true of polytopes in higher dimensions.)

The rectified polyhedron turns out to be expressible as the intersection of the original platonic solid with an appropriately scaled concentric version of its dual. For this reason, its name is a combination of the names of the original and the dual:

• The tetrahedron is its own dual, and its rectification is the tetratetrahedron, better known as the octahedron.
• The octahedron and the cube are each other's dual, and their rectification is the cuboctahedron.
• The icosahedron and the dodecahedron are duals, and their rectification is the icosidodecahedron.

Examples

Family	Parent	Rectification	Dual
[p,q]
[3,3]	Tetrahedron	Octahedron	Tetrahedron
[4,3]	Cube	Cuboctahedron	Octahedron
[5,3]	Dodecahedron	Icosidodecahedron	Icosahedron
[6,3]	Hexagonal tiling	Trihexagonal tiling	Triangular tiling
[7,3]	Order-3 heptagonal tiling	Triheptagonal tiling	Order-7 triangular tiling
[4,4]	Square tiling	Square tiling	Square tiling
[5,4]	Order-4 pentagonal tiling	Tetrapentagonal tiling	Order-5 square tiling

In nonregular polyhedra

If a polyhedron is not regular, the edge midpoints surrounding a vertex may not be coplanar. However, a form of rectification is still possible in this case: every polyhedron has a polyhedral graph as its 1-skeleton, and from that graph one may form the medial graph by placing a vertex at each edge midpoint of the original graph, and connecting two of these new vertices by an edge whenever they belong to consecutive edges along a common face. The resulting medial graph remains polyhedral, so by Steinitz's theorem it can be represented as a polyhedron.

The Conway polyhedron notation equivalent to rectification is ambo, represented by a. Applying twice aa, (rectifying a rectification) is Conway's expand operation, e, which is the same as Johnson's cantellation operation, t_0,2 generated from regular polyhedral and tilings.

In 4-polytopes and 3D honeycomb tessellations

Each Convex regular 4-polytope has a rectified form as a uniform 4-polytope.

A regular 4-polytope {p,q,r} has cells {p,q}. Its rectification will have two cell types, a rectified {p,q} polyhedron left from the original cells and {q,r} polyhedron as new cells formed by each truncated vertex.

A rectified {p,q,r} is not the same as a rectified {r,q,p}, however. A further truncation, called bitruncation, is symmetric between a 4-polytope and its dual. See Uniform 4-polytope#Geometric derivations.

Examples

Family	Parent	Rectification	Birectification (Dual rectification)	Trirectification (Dual)
[p,q,r]	{p,q,r}	r{p,q,r}	2r{p,q,r}	3r{p,q,r}
[3,3,3]	5-cell	rectified 5-cell	rectified 5-cell	5-cell
[4,3,3]	tesseract	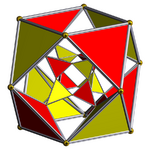rectified tesseract	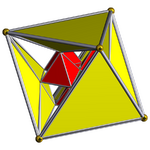Rectified 16-cell (24-cell)	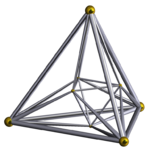16-cell
[3,4,3]	24-cell	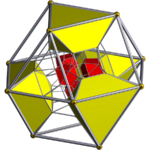rectified 24-cell	rectified 24-cell	24-cell
[5,3,3]	120-cell	rectified 120-cell	rectified 600-cell	600-cell
[4,3,4]	Cubic honeycomb	Rectified cubic honeycomb	Rectified cubic honeycomb	Cubic honeycomb
[5,3,4]	Order-4 dodecahedral	Rectified order-4 dodecahedral	Rectified order-5 cubic	Order-5 cubic

Degrees of rectification

A first rectification truncates edges down to points. If a polytope is regular, this form is represented by an extended Schläfli symbol notation t₁{p,q,...} or r{p,q,...}.

A second rectification, or birectification, truncates faces down to points. If regular it has notation t₂{p,q,...} or 2r{p,q,...}. For polyhedra, a birectification creates a dual polyhedron.

Higher degree rectifications can be constructed for higher dimensional polytopes. In general an n-rectification truncates n-faces to points.

If an n-polytope is (n-1)-rectified, its facets are reduced to points and the polytope becomes its dual.

Notations and facets

There are different equivalent notations for each degree of rectification. These tables show the names by dimension and the two type of facets for each.

Regular polygons

Facets are edges, represented as {}.

name {p}	Coxeter diagram	t-notation Schläfli symbol	Vertical Schläfli symbol
			Name	Facet-1	Facet-2
Parent		t0{p}	{p}	{}
Rectified		t1{p}	{p}		{}

Regular polyhedra and tilings

Facets are regular polygons.

name {p,q}	Coxeter diagram	t-notation Schläfli symbol	Vertical Schläfli symbol
			Name	Facet-1	Facet-2
Parent	=	t0{p,q}	{p,q}	{p}
Rectified	=	t1{p,q}	r{p,q} = [math]\displaystyle{ \begin{Bmatrix} p \\ q \end{Bmatrix} }[/math]	{p}	{q}
Birectified	=	t2{p,q}	{q,p}		{q}

Regular Uniform 4-polytopes and honeycombs

Facets are regular or rectified polyhedra.

name {p,q,r}	Coxeter diagram	t-notation Schläfli symbol	Extended Schläfli symbol
			Name	Facet-1	Facet-2
Parent		t0{p,q,r}	{p,q,r}	{p,q}
Rectified		t1{p,q,r}	[math]\displaystyle{ \begin{Bmatrix} p \ \ \\ q , r \end{Bmatrix} }[/math] = r{p,q,r}	[math]\displaystyle{ \begin{Bmatrix} p \\ q \end{Bmatrix} }[/math] = r{p,q}	{q,r}
Birectified (Dual rectified)		t2{p,q,r}	[math]\displaystyle{ \begin{Bmatrix} q , p \\ r \ \ \end{Bmatrix} }[/math] = r{r,q,p}	{q,r}	[math]\displaystyle{ \begin{Bmatrix} q \\ r \end{Bmatrix} }[/math] = r{q,r}
Trirectified (Dual)		t3{p,q,r}	{r,q,p}		{r,q}

Regular 5-polytopes and 4-space honeycombs

Facets are regular or rectified 4-polytopes.

name {p,q,r,s}	Coxeter diagram	t-notation Schläfli symbol	Extended Schläfli symbol
			Name	Facet-1	Facet-2
Parent		t0{p,q,r,s}	{p,q,r,s}	{p,q,r}
Rectified		t1{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} p \ \ \ \ \ \\ q , r , s \end{Bmatrix} }[/math] = r{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} p \ \ \\ q , r \end{Bmatrix} }[/math] = r{p,q,r}	{q,r,s}
Birectified (Birectified dual)		t2{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} q , p \\ r , s \end{Bmatrix} }[/math] = 2r{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} q , p \\ r \ \ \end{Bmatrix} }[/math] = r{r,q,p}	[math]\displaystyle{ \begin{Bmatrix} q \ \ \\ r , s \end{Bmatrix} }[/math] = r{q,r,s}
Trirectified (Rectified dual)		t3{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} r , q , p \\ s \ \ \ \ \ \end{Bmatrix} }[/math] = r{s,r,q,p}	{r,q,p}	[math]\displaystyle{ \begin{Bmatrix} r , q \\ s \ \ \end{Bmatrix} }[/math] = r{s,r,q}
Quadrirectified (Dual)		t4{p,q,r,s}	{s,r,q,p}		{s,r,q}

See also

• Dual polytope
• Quasiregular polyhedron
• List of regular polytopes
• Truncation (geometry)
• Conway polyhedron notation

References

• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)

External links

• Olshevsky, George. "Rectification". Glossary for Hyperspace. Archived from the original on 4 February 2007. https://web.archive.org/web/20070204075028/members.aol.com/Polycell/glossary.html#Rectification.