Section formula

In coordinate geometry, the Section formula is a formula used to find the ratio in which a line segment is divided by a point internally or externally. It is used to find out the centroid, incenter and excenters of a triangle. In physics, it is used to find the center of mass of systems, equilibrium points, etc.

Internal Divisions

Internal division with section formula

If point P (lying on AB) divides the line segment AB joining the points $\mathrm{A}(x_1,y_1)$ and $\mathrm{B}(x_2,y_2)$ in the ratio m:n, then

$P=(\frac{m{x}_2+n{x}_1}{m+n},\frac{m{y}_2+n{y}_1}{m+n})$

The ratio m:n can also be written as $m/n:1$, or $k:1$, where $k=m/n$. So, the coordinates of point $P$ dividing the line segment joining the points $\mathrm{A}(x_1,y_1)$ and $\mathrm{B}(x_2,y_2)$ are:

$(\frac{m{x}_2+n{x}_1}{m+n},\frac{m{y}_2+n{y}_1}{m+n})$

$=(\frac{\frac{m}{n}{x}_2+x_1}{\frac{m}{n}+1},\frac{\frac{m}{n}{y}_2+y_1}{\frac{m}{n}+1})$

$=(\frac{k{x}_2+x_1}{k+1},\frac{k{y}_2+y_1}{k+1})$

Similarly, the ratio can also be written as $k:k-1$, and the coordinates of P are $((1-k)x_1+k{x}_2,(1-k)y_1+k{y}_2)$.

Proof

Triangles $PAQ\sim BPC$.

$\begin{array}{r}\frac{AP}{BP}=\frac{AQ}{CP}=\frac{PQ}{BC}\\ \frac{m}{n}=\frac{x-x_1}{x_2-x}=\frac{y-y_1}{y_2-y}\\ m{x}_2-mx=nx-n{x}_1,m{y}_2-my=ny-n{y}_1\\ mx+nx=m{x}_2+n{x}_1,my+ny=m{y}_2+n{y}_1\\ (m+n)x=m{x}_2+n{x}_1,(m+n)y=m{y}_2+n{y}_1\\ x=\frac{m{x}_2+n{x}_1}{m+n},y=\frac{m{y}_2+n{y}_1}{m+n}\\ \end{array}$

External Divisions

External division with section formula

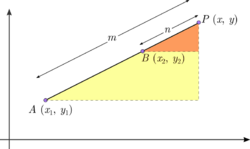
If a point P (lying on the extension of AB) divides AB in the ratio m:n then

$P=(\frac{m{x}_2-n{x}_1}{m-n},\frac{m{y}_2-n{y}_1}{m-n})$

Proof

Triangles $PAC\sim PBD$ (Let C and D be two points where A & P and B & P intersect respectively). Therefore ∠ACP = ∠BDP

$\begin{array}{r}\frac{AB}{BP}=\frac{AC}{BD}=\frac{PC}{PD}\\ \frac{m}{n}=\frac{x-x_1}{x-x_2}=\frac{y-y_1}{y-y_2}\\ mx-m{x}_2=nx-n{x}_1,my-m{y}_2=ny-n{y}_1\\ mx-nx=m{x}_2-n{x}_1,my-ny=m{y}_2-n{y}_1\\ (m-n)x=m{x}_2-n{x}_1,(m-n)y=m{y}_2-n{y}_1\\ x=\frac{m{x}_2-n{x}_1}{m-n},y=\frac{m{y}_2-n{y}_1}{m-n}\\ \end{array}$

Midpoint formula

Main article: Midpoint

The midpoint of a line segment divides it internally in the ratio $1:1$. Applying the Section formula for internal division:

$$P=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$$

Derivation

$P=(\frac{m{x}_2+n{x}_1}{m+n},\frac{m{y}_2+n{y}_1}{m+n})$

$=(\frac{1\cdot x_1+1\cdot x_2}{1+1},\frac{1\cdot y_1+1\cdot y_2}{1+1})$

$=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$

Centroid

Centroid of a triangle

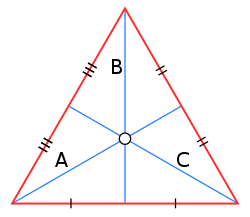
The centroid of a triangle is the intersection of the medians and divides each median in the ratio $2:1$. Let the vertices of the triangle be $A(x_1,y_1)$, $B(x_2,y_2)$ and $C(x_3,y_3)$. So, a median from point A will intersect BC at $(\frac{x_2+x_3}{2},\frac{y_2+y_3}{2})$. Using the section formula, the centroid becomes:

$$(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})$$

In 3-Dimensions

Let A and B be two points with Cartesian coordinates (x₁, y₁, z₁) and (x₂, y₂, z₂) and P be a point on the line through A and B. If $AP:PB=m:n$. Then the section formulae give the coordinates of P as

$(\frac{m{x}_2+n{x}_1}{m+n},\frac{m{y}_2+n{y}_1}{m+n},\frac{m{z}_2+n{z}_1}{m+n})$

If, instead, P is a point on the line such that $AP:PB=k:1-k$, its coordinates are $((1-k)x_1+k{x}_2,(1-k)y_1+k{y}_2,(1-k)z_1+k{z}_2)$.

In vectors

The position vector of a point P dividing the line segment joining the points A and B whose position vectors are $\overrightarrow{a}$ and $\overrightarrow{b}$

1. in the ratio $m:n$ internally, is given by $\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}$
2. in the ratio $m:n$ externally, is given by $\frac{m\overrightarrow{b}-n\overrightarrow{a}}{m-n}$

See also

• Cross-section Formula
• Distance Formula
• Midpoint Formula

External links

• section-formula by GeoGebra