Snub rhombicuboctahedron
From HandWiki
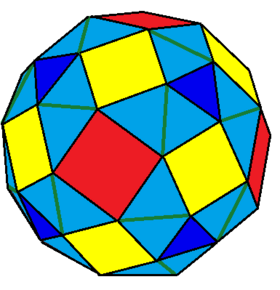
| Snub rhombicuboctahedron | |
|---|---|
| |
| Schläfli symbol | srr{4,3} = [math]\displaystyle{ sr\begin{Bmatrix} 4 \\ 3 \end{Bmatrix} }[/math] |
| Conway notation | saC |
| Faces | 74: 8+48 {3} 6+12 {4} |
| Edges | 120 |
| Vertices | 48 |
| Symmetry group | O, [4,3]+, (432) order 24 |
| Dual polyhedron | Pentagonal tetracontoctahedron |
| Properties | convex, chiral |
The snub rhombicuboctahedron is a polyhedron, constructed as a truncated rhombicuboctahedron. It has 74 faces: 18 squares, and 56 triangles. It can also be called the Conway snub cuboctahedron in but will be confused with the Coxeter snub cuboctahedron, the snub cube.
Related polyhedra
The snub rhombicuboctahedron can be seen in sequence of operations from the cuboctahedron.
| Name | Cubocta- hedron |
Truncated cubocta- hedron |
Snub cubocta- hedron |
Truncated rhombi- cubocta- hedron |
Snub rhombi- cubocta- hedron |
|---|---|---|---|---|---|
| Coxeter | CO (rC) | tCO (trC) | sCO (srC) | trCO (trrC) | srCO (htrrC) |
| Conway | aC | taC = bC | sC | taaC = baC | saC |
| Image | 
|
|

|

|

|
| Conway | jC | mC | gC | maC | gaC |
| Dual | 
|

|

|

|

|
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5
External links
- George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input
 |

