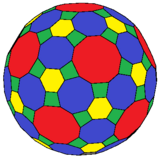
Truncated rhombicosidodecahedron
| Truncated rhombicosidodecahedron | |
|---|---|
| |
| Schläfli symbol | trr{5,3} = [math]\displaystyle{ tr\begin{Bmatrix} 5 \\ 3 \end{Bmatrix} }[/math] |
| Conway notation | taD = baD |
| Faces | 122: 60 {4} 20 {6} 30 {8} 12 {10} |
| Edges | 360 |
| Vertices | 240 |
| Symmetry group | Ih, [5,3], (*532) order 120 |
| Rotation group | I, [5,3]+, (532), order 60 |
| Dual polyhedron | Disdyakis hexecontahedron
|
| Properties | convex |
In geometry, the truncated rhombicosidodecahedron is a polyhedron, constructed as a truncated rhombicosidodecahedron. It has 122 faces: 12 decagons, 30 octagons, 20 hexagons, and 60 squares.
Other names
- Truncated small rhombicosidodecahedron
- Beveled icosidodecahedron
Zonohedron
As a zonohedron, it can be constructed with all but 30 octagons as regular polygons. It is 2-uniform, with 2 sets of 120 vertices existing on two distances from its center.
This polyhedron represents the Minkowski sum of a truncated icosidodecahedron, and a rhombic triacontahedron.[1]
Related polyhedra
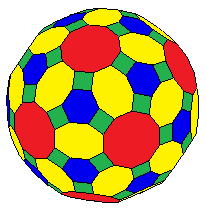
The truncated icosidodecahedron is similar, with all regular faces, and 4.6.10 vertex figure. Also see the truncated rhombirhombicosidodecahedron.
| truncated icosidodecahedron | Truncated rhombicosidodecahedron |
|---|---|
 4.6.10 |
 4.8.10 and 4.6.8 |
The truncated rhombicosidodecahedron can be seen in sequence of rectification and truncation operations from the icosidodecahedron. A further alternation step leads to the snub rhombicosidodecahedron.
| Name | Icosidodeca- hedron |
Rhomb- icosidodeca- hedron |
Truncated rhomb- icosidodeca- hedron |
Snub rhomb- icosidodeca- hedron |
|---|---|---|---|---|
| Coxeter | ID (rD) | rID (rrD) | trID (trrD) | srID (htrrD) |
| Conway | aD | aaD = eD | taaD = baD | saD |
| Image | 
|
|
|
|
| Conway | jD | oD | maD | gaD |
| Dual | 
|
|
|
|
See also
References
- ↑ Eppstein (1996)
- Eppstein, David (1996). "Zonohedra and zonotopes". Mathematica in Education and Research 5 (4): 15–21. http://www.ics.uci.edu/~eppstein/junkyard/ukraine/ukraine.html.
- Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
External links
- George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input
 |  |
