Software:DrGeo

GNU Dr. Geo

Original author(s)	Hilaire Fernandes
Initial release	December 31, 1996 (1996-12-31)
Stable release	23.12 / December 20, 2023 (2023-12-20)
Written in	Cuis Smalltalk, Smalltalk
Operating system	Linux, Mac OS X, Windows, Sugar
Type	Interactive geometry software
License	GPL
Website	www.gnu.org/s/dr-geo

GNU Dr. Geo is an interactive geometry software that allows its users to design & manipulate interactive geometric sketches, including dynamic models of Physics. It is free software (source code, translations, icons and installer are released under GNU GPL license), created by Hilaire Fernandes, it is part of the GNU project. It runs over a Morphic graphic system (which means that it runs on Linux, Mac OS, Windows, Android). Dr. Geo was initially developed in C++, then in various versions of Smalltalk with Squeak, Etoys (programming language) for One Laptop per Child Pharo then Cuis-Smalltalk.

Objects

Dr. Geo manipulates different kinds of objects such as points, lines, circles, vector, values, geometric transformations, scripts.

Points

Dr. Geo has several kinds of points: a free point, which can be moved with the mouse (but may be attached to a curve) and a point given by its coordinates.

Points can also be created as the intersection of 2 curves or as the midpoint of a segment.

Lines

Dr. Geo is equipped with the classic line, ray, segment and vector.

Other curvilinear objects include circles (defined by 2 points, a center and segment or a radius), arcs (defined by three points or center and angle), polygons (regular or not, defined by end points), and loci.

Transformations

Besides the parallel and perpendicular line through a point.

Dr. Geo can apply to a point or a line one of these transformations:

1. reflexion
2. symmetry
3. translation
4. rotation
5. homothety

Macro-construction

Dr. Geo comes with macro-construction: a way to teach Dr. Geo new constructions. It allows to add new objects to Dr. Geo: new transformations like circle inversion, tedious constructions involving a lot of intermediate objects or constructions involving script (also named macro-script).

When some objects, called final depend on other objects, called initial, it is possible to create a complex construction deducing the final objects from the user-given initial objects. This is a macro-construction, a graph of interdependent objects.

Programming

Access to user programming is at the essence of Dr. Geo: from the software, the user can directly read, study, modify and redistribute modified version of Dr. Geo. Additionally, scripting embedded in sketch is proposed.

Dr. Geo source code is Smalltalk. It is also the language used for user programming: to extend Dr. Geo with arbitrary computing operations (Smalltalk script) and to define a geometric sketch entirely with programming instructions (Smalltalk sketch).

Dr. Geo is shipped with its source code and the developer tools. Therefore its code can be edited and recompiled from Dr. Geo while it is functioning. This design, inherited from Smalltalk, makes easy to test new ideas and new designs.

Smalltalk script

Curve and its tangent computed with Smalltalk scripts

A script is a first class object defined along Dr. Geo code. It comes with zero, one or several arguments, from types selected when defining the script. When an instance of a script is plugged in a canvas, the user first selects its arguments in the canvas with mouse clicks, then the position in the canvas of the script output. The script is updated at each canvas computation. Scripts can be used in cascade, with one as the argument of another one. Script are designed to be used in two different ways:

1. To output an object (i.e. a numeric value) and to show its result in the canvas. This result can be used when building subsequent objects (geometric or script).
2. To access objects in the canvas: model (MathItem) or their view (Costume) for arbitrary uses and modifications. For example to modify the color of an object given the result to a computation.

Live script editing

From the script, the arguments model are reached with the messages #arg1, #arg2, etc. The arguments view are reached with the messages #costume1, #costume2, etc.

The computation of the script is done in its #compute method. For example, to calculate the square of a number, la méthode

compute
"returns the square of a number"
^ self arg1 valueItem squared

creates a numeric object, whose value is the square of its first and unique argument of type number object. Whenever the first number is changed, the script returned value changes too.

Smalltalk sketch

Smalltalk sketch editor

Dr. Geo Smalltalk sketches are sketches entirely defined in the Smalltalk language. This is not about constructing a sketch with the Dr. Geo graphical interface, but about describing a sketch with the Smalltalk language. A programming interface with an easy and light syntax is provided.

Smalltalk itself is a high level language, carefully crafted iteratively for about 10 years at Palo Alto Research Center. When a sketch is described with Smalltalk code, all the features of the language are used: object oriented programming, variable, collection, iterator, randomness to get a slightly different sketch at each execution.

A Smalltalk sketch is edited and tested with the Smalltalk sketch editor. Such sketch can be debugged and executed step-by-step. Its code is saved, as any source code, to an external text file encoded with UTF-8, to support native language.

Sierpinski triangle

Here is how to program a Sierpinski triangle recursively. Its red external summit is mobile.

Computed interactive Sierpinski triangle

| triangle c |
c := DrGeoSketch new.
triangle := [:s1 :s2 :s3 :n |
    c segment: s1 to: s2; segment: s2 to: s3; segment: s3 to: s1.
    n > 0 ifTrue: [
        triangle
            value: s1
            value: (c middleOf: s1 and: s2) hide
            value: (c middleOf: s1 and: s3) hide
            value: n-1.
        triangle
            value: (c middleOf: s1 and: s2) hide
            value: s2
            value: (c middleOf: s2 and: s3) hide
            value: n-1.
        triangle
            value: (c middleOf: s1 and: s3) hide
            value: (c middleOf: s2 and: s3) hide
            value: s3
            value: n-1]].
triangle value: 0@3 value:  4@ -3 value: -4@ -3 value: 3.
(c point: 0@3) show

Fibonacci spiral

A Fibonacci spiral programmed with geometric transformations (rotation, translation and homothety). The points a and b of the resulting interactive sketch are mobile.

Computed interactive Fibonacci spiral

|canvas shape alfa fibo a b m s|
canvas := DrGeoSketch new.
alfa := (canvas freeValue: -90 degreesToRadians) hide.
shape := [:c :o :f| | e p |
	e := (canvas rotate: o center: c angle: alfa) hide.
	(canvas arcCenter: c from: o to: e) large.
	p := canvas translate: e vector: (canvas vector: c to: o) hide.
	(canvas polygon: { c. o. p hide. e }) name: f.
	e].
fibo := [ ].
fibo := [ :f :o :c :k | | e f1 f2 f3 c2|
"f1: term Fn-1, f2: term Fn, o & c: origin and center of spiral arm
e: extremity of the spiral arm"
	f1 := f first.
	f2 := f second.
	f3 := f1 + f2.
	e := shape value: c value: o value: f3.	
	c2 := (canvas scale: c center: e factor: f3 / f2) hide.
	k > 0 ifTrue: [ fibo value: {f2. f3} value: e value: c2 value: k - 1 ]].

a := canvas point: 1@0.
b := canvas point: -1 @0.
m := (canvas middleOf: a and: b) hide.
s := shape value: m value: a value: 1.
shape value: m value: s value: 1.
fibo value: {1. 2} value: b value: a value: 10

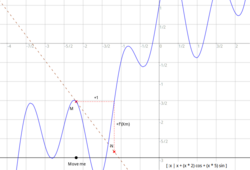
Newton-Raphson algorithm

Smalltalk sktech can be used to design interactive sketch illustrating a numerical analysis method. Here the Newton-Raphson algorithm in a 5 steps iteration.

Computed interactive Newton-Raphson algorithm

| sketch f df xn ptA ptB|
sketch := DrGeoSketch new axesOn.
xn := 2.
f := [ :x | x cos + x ].
"Derivate number"
df := [ :x | (f value: x + 1e-8) - (f value: x) * 1e8].
sketch plot: f from: -20 to: 20.
ptA := (sketch point: xn@0) large; name: 'Drag me'.
5 timesRepeat: [ 
	ptB := sketch 
		point: [ :pt | pt point x @ (f value: pt point x)] 
		parent: ptA.
	ptB hide.
	(sketch segment: ptA to: ptB) dotted forwardArrow .
	ptA := sketch point: [:pt | 
		| x |
		x := pt point x.
		x - ( (f value: x) / (df value: x) )  @ 0 ] parent: ptB.
	ptA hide.
	(sketch segment: ptB to: ptA) dotted forwardArrow].

Locale languages

Smalltalk sketch can be coded in native languages, currently in French and Spanish. More native languages can be added.

Awards

• ESUG Innovation Technology Awards (Amsterdam, 2008)
• AFUL Free Software Awards (Paris, 2000)

See also

• Compass-and-straightedge construction
• Interactive geometry software