Locus (mathematics)

From HandWiki
Short description: Set of points that satisfy some specified conditions
Each curve in this example is a locus defined as the conchoid of the point P and the line l. In this example, P is 8 cm from l.

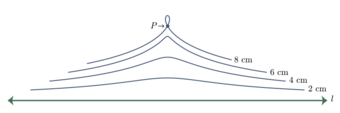
In geometry, a locus (plural: loci) (Latin word for "place", "location") is a set of all points (commonly, a line, a line segment, a curve or a surface), whose location satisfies or is determined by one or more specified conditions.[1][2]

The set of the points that satisfy some property is often called the locus of a point satisfying this property. The use of the singular in this formulation is a witness that, until the end of the 19th century, mathematicians did not consider infinite sets. Instead of viewing lines and curves as sets of points, they viewed them as places where a point may be located or may move.

History and philosophy

Until the beginning of the 20th century, a geometrical shape (for example a curve) was not considered as an infinite set of points; rather, it was considered as an entity on which a point may be located or on which it moves. Thus a circle in the Euclidean plane was defined as the locus of a point that is at a given distance of a fixed point, the center of the circle. In modern mathematics, similar concepts are more frequently reformulated by describing shapes as sets; for instance, one says that the circle is the set of points that are at a given distance from the center.[3]

In contrast to the set-theoretic view, the old formulation avoids considering infinite collections, as avoiding the actual infinite was an important philosophical position of earlier mathematicians.[4][5]

Once set theory became the universal basis over which the whole mathematics is built,[6] the term of locus became rather old-fashioned.[7] Nevertheless, the word is still widely used, mainly for a concise formulation, for example:

More recently, techniques such as the theory of schemes, and the use of category theory instead of set theory to give a foundation to mathematics, have returned to notions more like the original definition of a locus as an object in itself rather than as a set of points.[5]

Examples in plane geometry

Examples from plane geometry include:

  • The set of points equidistant from two points is a perpendicular bisector to the line segment connecting the two points.[8]
  • The set of points equidistant from two intersecting lines is the union of their two angle bisectors.
  • All conic sections are loci:[9]
    • Circle: the set of points at constant distance (the radius) from a fixed point (the center).
    • Parabola: the set of points equidistant from a fixed point (the focus) and a line (the directrix).
    • Hyperbola: the set of points for each of which the absolute value of the difference between the distances to two given foci is a constant.
    • Ellipse: the set of points for each of which the sum of the distances to two given foci is a constant

Other examples of loci appear in various areas of mathematics. For example, in complex dynamics, the Mandelbrot set is a subset of the complex plane that may be characterized as the connectedness locus of a family of polynomial maps.

Proof of a locus

To prove a geometric shape is the correct locus for a given set of conditions, one generally divides the proof into two stages: the proof that all the points that satisfy the conditions are on the given shape, and the proof that all the points on the given shape satisfy the conditions.[10]

Examples

(distance PA) = 3.(distance PB)

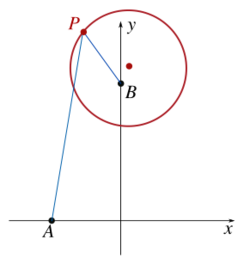
First example

Find the locus of a point P that has a given ratio of distances k = d1/d2 to two given points.

In this example k = 3, A(−1, 0) and B(0, 2) are chosen as the fixed points.

P(x, y) is a point of the locus
[math]\displaystyle{ \Leftrightarrow |PA| = 3 |PB| }[/math]
[math]\displaystyle{ \Leftrightarrow |PA|^2 = 9 |PB|^2 }[/math]
[math]\displaystyle{ \Leftrightarrow (x + 1)^2 + (y - 0)^2 = 9(x - 0)^2 + 9(y - 2)^2 }[/math]
[math]\displaystyle{ \Leftrightarrow 8(x^2 + y^2) - 2x - 36y + 35 = 0 }[/math]
[math]\displaystyle{ \Leftrightarrow \left(x - \frac18\right)^2 + \left(y - \frac94\right)^2 = \frac{45}{64}. }[/math]

This equation represents a circle with center (1/8, 9/4) and radius [math]\displaystyle{ \tfrac{3}{8}\sqrt{5} }[/math]. It is the circle of Apollonius defined by these values of k, A, and B.

Second example

Locus of point C

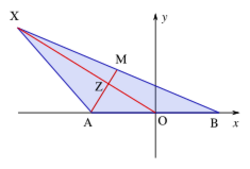
A triangle ABC has a fixed side [AB] with length c. Determine the locus of the third vertex C such that the medians from A and C are orthogonal.

Choose an orthonormal coordinate system such that A(−c/2, 0), B(c/2, 0). C(x, y) is the variable third vertex. The center of [BC] is M((2x + c)/4, y/2). The median from C has a slope y/x. The median AM has slope 2y/(2x + 3c).

The locus is a circle
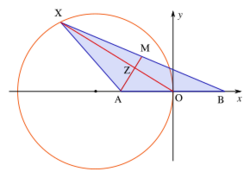
C(x, y) is a point of the locus
[math]\displaystyle{ \Leftrightarrow }[/math] the medians from A and C are orthogonal
[math]\displaystyle{ \Leftrightarrow \frac{y}{x} \cdot \frac{2y}{2x + 3c} = -1 }[/math]
[math]\displaystyle{ \Leftrightarrow 2 y^2 + 2x^2 + 3c x = 0 }[/math]
[math]\displaystyle{ \Leftrightarrow x^2 + y^2 + (3c/2) x = 0 }[/math]
[math]\displaystyle{ \Leftrightarrow (x + 3c/4)^2 + y^2 = 9c^2/16. }[/math]

The locus of the vertex C is a circle with center (−3c/4, 0) and radius 3c/4.

Third example

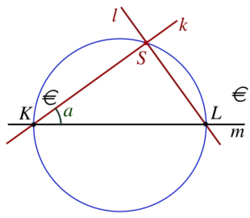
The intersection point of the associated lines k and l describes the circle

A locus can also be defined by two associated curves depending on one common parameter. If the parameter varies, the intersection points of the associated curves describe the locus.

In the figure, the points K and L are fixed points on a given line m. The line k is a variable line through K. The line l through L is perpendicular to k. The angle [math]\displaystyle{ \alpha }[/math] between k and m is the parameter. k and l are associated lines depending on the common parameter. The variable intersection point S of k and l describes a circle. This circle is the locus of the intersection point of the two associated lines.

Fourth example

A locus of points need not be one-dimensional (as a circle, line, etc.). For example,[1] the locus of the inequality 2x + 3y – 6 < 0 is the portion of the plane that is below the line of equation 2x + 3y – 6 = 0.

See also

References

  1. ↑ 1.0 1.1 James, Robert Clarke; James, Glenn (1992), Mathematics Dictionary, Springer, p. 255, ISBN 978-0-412-99041-0, https://books.google.com/books?id=UyIfgBIwLMQC&pg=PA255 .
  2. ↑ Whitehead, Alfred North (1911), An Introduction to Mathematics, H. Holt, p. 121, ISBN 978-1-103-19784-2, https://books.google.com/books?id=0Ko-AAAAYAAJ&pg=PA121 .
  3. ↑ Cooke, Roger L. (2012), "38.3 Topology", The History of Mathematics: A Brief Course (3rd ed.), John Wiley & Sons, ISBN 9781118460290, https://books.google.com/books?id=CFDaj0WUvM8C&pg=PT534, "The word locus is one that we still use today to denote the path followed by a point moving subject to stated constraints, although, since the introduction of set theory, a locus is more often thought of statically as the set of points satisfying a given collection." 
  4. ↑ Bourbaki, N. (2013), Elements of the History of Mathematics, Springer, p. 26, ISBN 9783642616938, https://books.google.com/books?id=4JprCQAAQBAJ&pg=PA26, "the classical mathematicians carefully avoided introducing into their reasoning the 'actual infinity'" .
  5. ↑ 5.0 5.1 Borovik, Alexandre (2010), "6.2.4 Can one live without actual infinity?", Mathematics Under the Microscope: Notes on Cognitive Aspects of Mathematical Practice, American Mathematical Society, p. 124, ISBN 9780821847619, https://books.google.com/books?id=hEPSAwAAQBAJ&pg=PA124 .
  6. ↑ Mayberry, John P. (2000), The Foundations of Mathematics in the Theory of Sets, Encyclopedia of Mathematics and its Applications, 82, Cambridge University Press, p. 7, ISBN 9780521770347, https://books.google.com/books?id=mP1ofko7p6IC&pg=PA7, "set theory provides the foundations for all mathematics" .
  7. ↑ Ledermann, Walter; Vajda, S. (1985), Combinatorics and Geometry, Part 1, Handbook of Applicable Mathematics, 5, Wiley, p. 32, ISBN 9780471900238, "We begin by explaining a slightly old-fashioned term" .
  8. ↑ George E. Martin, The Foundations of Geometry and the Non-Euclidean Plane, Springer-Verlag, 1975.
  9. ↑ Hamilton, Henry Parr (1834), An Analytical System of Conic Sections: Designed for the Use of Students, Springer .
  10. ↑ G. P. West, The new geometry: form 1.



Retrieved from "https://handwiki.org/wiki/index.php?title=Locus_(mathematics)&oldid=3387855"