Spidron

From HandWiki
This article discusses the geometric figure; for the science-fiction character see Spidron (character).
First spidron created by Dániel Erdély in 1979, consisting of equilateral triangles and the symmetrical obtuse isosceles triangles which together form right triangles

In geometry, a spidron is a continuous flat geometric figure composed entirely of triangles, where, for every pair of joining triangles, each has a leg of the other as one of its legs, and neither has any point inside the interior of the other. A deformed spidron is a three-dimensional figure sharing the other properties of a specific spidron, as if that spidron were drawn on paper, cut out in a single piece, and folded along a number of legs.

Origin and development

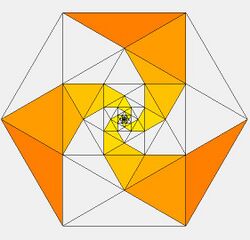
Spidron hexagon, similar to the 1979 image
A standard spidron consists of two alternating, adjoining sequences of equilateral and isosceles triangles.[1]

It was first modelled in 1979 by Dániel Erdély, as a homework presented to Ernő Rubik, for Rubik's design class, at the Hungarian University of Arts and Design (now: Moholy-Nagy University of Art and Design). Erdély also gave the name "Spidron" to it, when he discovered it in the early 70s.[1] The name originates from the English names of spider and spiral, because the shape is reminiscent of a spider web.[2] The term ends with the affix "-on" as in polygon.[1]

A spidron is a plane figure consisting of an alternating sequence of equilateral and isosceles (30°, 30°, 120°) triangles. Within the figure, one side of a regular triangle coincides with one of the sides of an isosceles triangle, while another side coincides with the hypotenuse of another, smaller isosceles triangle. The sequence can be repeated any number of times in the direction of the smaller and smaller triangles, and the entire figure is centrally projected through the mid-point of the base of the largest unilateral triangle.[3]

In his initial work Erdély started with a hexagon. He combined every corner with the after-next one. In his mathematical analysis of spidrons Stefan Stenzhorn demonstrated that it is possible to create a spidron with every regular Polygon greater than four. Furthermore, you can vary the number of points to the next combination. Stenzhorn reasoned that after all the initial hexagon-spidron is just the special case of a general spidron.[4]

In a two-dimensional plane a tessellation with hexagon-spidrons is possible. The form is known from many works by M.C. Escher, who devoted himself to such bodies of high symmetry. Due to their symmetry spidrons are also an interesting object for mathematicians.

The spidrons can appear in a very large number of versions, and the different formations make possible the development of a great variety of plane, spatial and mobile applications. These developments are suitable to perform aesthetic and practical functions that are defined in advance by the consciously selected arrangements of all the possible characteristics of symmetry. The spidron system is under the protection of several know-how and industrial pattern patents; Spidron is a registered trademark. It was awarded a gold medal at the exhibition Genius Europe in 2005. It has been presented in a number of art magazines, conferences and international exhibitions. During the last two years it has also appeared, in several versions, as a public area work. Since spidron-system is the personal work by Dániel Erdély but in the development of the individual formations he worked together with several Hungarian, Dutch, Canadian and American colleagues, the exhibition is a collective product in a sense, several works and developments are a result of an international team-work.

The spidron is constructed from two semi-spidrons sharing a long side, with one rotated 180 degrees to the other. If the second semi-spidron is reflected in the long side instead of rotated, the result is a "hornflake". Deformed spidrons or hornflakes can be used to construct polyhedra called spidrohedra or hornhedra. Some of these polyhedra are space fillers.[5]

A semi-spidron may have infinitely many triangles. Such spidronized polyhedra have infinitely many faces and are examples of apeirohedra.

Octagon spidron created by Stenzhorn (2009)

Practical use

Considering the use of spidrons Daniel Erdély enumerated several possible applications:

It has been raised repeatedly that several layers of spidron reliefs could be used as shock dampers or crumple zones in vehicles. Its space-filling properties make it suitable for the construction of building blocks or toys. The surface could be used to create an adjustable acoustic wall or a system of solar cells that follow the sun in a simple manner. Various folding buildings and static structures could also be developed on the basis of my geometric investigation which may have utility in space travel.[3]

See also

References

  1. ↑ 1.0 1.1 1.2 Peterson, Ivars (2006). "Swirling Seas, Crystal Balls". ScienceNews.org. http://www.sciencenews.org/articles/20061021/bob11.asp. 
  2. ↑ "Spidrons", Jugend-forscht.de (in German).
  3. ↑ 3.0 3.1 Erdély, Daniel (2004). "Concept of the Spidron System". http://matserv.pmmf.hu/hajtas/docs/2/Spidron_EN.pdf.  In: Proceedings of Sprout-Selecting Conference: Computer Algebra Systems and Dynamic Geometry Systems in Mathematics Teaching. C. Sárvári, ed. University of Pécs, Pécs, Hungary.
  4. ↑ [1][yes|permanent dead link|dead link}}]. Mathematical description of spidrons by Stefan Stenzhorn (in German).
  5. ↑ Erdély, Daniel.(2000). "Spidron System". Symmetry: Culture and Science. Vol. 11, Nos. 1-4. pp.307-316.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Spidron&oldid=3016120"