Still life (cellular automaton)
In Conway's Game of Life and other cellular automata, a still life is a pattern that does not change from one generation to the next. The term comes from the art world where a still life painting or photograph depicts an inanimate scene. In cellular automata, a still life can be thought of as an oscillator with unit period.[1]
Classification
A pseudo still life consists of two or more adjacent islands (connected components) which can be partitioned (either individually or as sets) into non-interacting subparts, which are also still lifes. This compares with a strict still life, which may not be partitioned in this way. A strict still life may have only a single island, or it may have multiple islands that depend on one another for stability, and thus cannot be decomposed. The distinction between the two is not always obvious, as a strict still life may have multiple connected components all of which are needed for its stability. However, it is possible to determine whether a still life pattern is a strict still life or a pseudo still life in polynomial time by searching for cycles in an associated skew-symmetric graph.[2]
Examples
There are many naturally occurring still lifes in Conway's Game of Life. A random initial pattern will leave behind a great deal of debris, containing small oscillators and a large variety of still lifes.
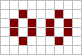
The most common still life (i.e. that most likely to be generated from a random initial state) is the block.[3] A pair of blocks placed side-by-side (or bi-block) is the simplest pseudo still life. Blocks are used as components in many complex devices, an example being the Gosper glider gun.
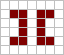
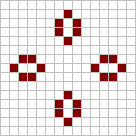
The second most common still life is the hive (or beehive).[3] Hives are frequently created in (non-interacting) sets of four, in a formation known as a honey farm.
The third most common still life is the loaf.[3] Loaves are often found together in a pairing known as a bi-loaf. Bi-loaves themselves are often created in a further (non-interacting) pairing known as a bakery. Two bakeries can extremely rarely form next to each other, forming a set of four loaves known as a tetraloaf alongside two more bi-loafs.
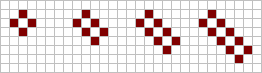
A tub consists of four live cells placed in a diamond shape around a central dead cell. Placing an extra live cell diagonally to the central cell gives another still life, known as a boat. Placing a further live cell on the opposite side gives yet another still life, known as a ship. A tub, a boat or a ship can be extended by adding a pair of live cells, to give a barge, a long-boat or a long-ship respectively. This extension can be repeated indefinitely, to give arbitrarily large structures.
A pair of boats can be combined to give another still life known as the boat tie (a pun on bow tie, which it superficially resembles). Similarly, a pair of ships can be combined into a ship tie.
Eaters
Still lifes can be used to modify or destroy other objects. A still life is called an eater when it can be used to absorb some other pattern (often a glider, spaceship, or the debris from a more complicated reaction) and returns to its original state after the collision. Many examples exist, with the most notable being the fish-hook (Also known as eater 1), which is capable of absorbing several types of spaceship. A similar device is the 'reflector', which alters the direction of an incoming spaceship. Oscillators with similar properties may also be called eaters or reflectors, but are more difficult to apply as they must be synchronized to the pattern they modify. Still life eaters and reflectors, on the other hand, work correctly regardless of the timing of the pattern they modify, as long as successive reactions occur with enough separation in time to allow the eater or reflector to recover its original shape.
Enumeration
The number of strict and pseudo still lifes in Conway's Game of Life existing for a given number of live cells has been documented up to a value of 34 (sequences A019473 and A056613 respectively in the On-Line Encyclopedia of Integer Sequences (OEIS)).[4][5]
| Live cells | Strict still lifes | Pseudo still lifes | Examples[1] |
|---|---|---|---|
| 1 | 0 | 0 | |
| 2 | 0 | 0 | |
| 3 | 0 | 0 | |
| 4 | 2 | 0 | Block, tub |
| 5 | 1 | 0 | Boat |
| 6 | 5 | 0 | Barge, beehive, carrier, ship, snake |
| 7 | 4 | 0 | Fishhook, loaf, long boat, python |
| 8 | 9 | 1 | Canoe, mango, long barge, pond |
| 9 | 10 | 1 | Hat, integral sign |
| 10 | 25 | 7 | Block on table, boat-tie, loop |
| 11 | 46 | 16 | |
| 12 | 121 | 55 | Ship-tie[citation needed] |
| 13 | 240 | 110 | |
| 14 | 619 | 279 | Bi-loaf[citation needed] |
| 15 | 1,353 | 620 | |
| 16 | 3,286 | 1,645 | |
| 17 | 7,773 | 4,067 | |
| 18 | 19,044 | 10,843 | |
| 20 | 112,243 | 70,637 | |
| 21 | 273,188 | 179,011 | |
| 22 | 672,172 | 462,086 | |
| 23 | 1,646,147 | 1,184,882 | |
| 24 | 4,051,732 | 3,069,135 | |
| 25 | 9,971,377 | 7,906,676 | |
| 26 | 24,619,307 | 20,463,274 | |
| 27 | 60,823,008 | 52,816,265 | |
| 28 | 150,613,157 | 136,655,095 | |
| 29 | 373,188,952 | 353,198,379 | |
| 30 | 926,068,847 | 914,075,620 | |
| 31 | 2,299,616,637 | 2,364,815,358 | |
| 32 | 5,716,948,683 | 6,123,084,116 | |
| 33 | 14,223,867,298 | 15,851,861,075 | |
| 34 | 35,422,864,104 | 41,058,173,683 |
Density
The problem of fitting an n×n region with a maximally dense still life has attracted attention as a test case for constraint programming.[6][7][8][9][10]
In the limit of an infinitely large grid, no more than half of the cells in the plane can be live.Cite error: Closing </ref> missing for <ref> tag Yorke-Smith provides a listing of known finite maximum-density patterns.[11]
References
- ↑ 1.0 1.1 "Still Life - from Eric Weisstein's Treasure Trove of Life C.A.". http://www.ericweisstein.com/encyclopedias/life/StillLife.html.
- ↑ Cook, Matthew (2003). "Still life theory". Santa Fe Institute Studies in the Sciences of Complexity, Oxford University Press. pp. 93–118.
- ↑ 3.0 3.1 3.2 Achim Flammenkamp. "Top 100 of Game-of-Life Ash Objects". http://wwwhomes.uni-bielefeld.de/achim/freq_top_life.html.
- ↑ Number of stable n-celled patterns ("still lifes") in Conway's game of Life (sequence A019473 in the OEIS).
- ↑ Number of n-celled pseudo-still-lifes in Conway's game of Life (sequence A056613 in the OEIS).
- ↑ Bosch, R. A. (1999). "Integer programming and Conway's game of Life". SIAM Review 41 (3): 594–604. doi:10.1137/S0036144598338252. Bibcode: 1999SIAMR..41..594B..
- ↑ Bosch, R. A. (2000). "Maximum density stable patterns in variants of Conway's game of Life". Operations Research Letters 27 (1): 7–11. doi:10.1016/S0167-6377(00)00016-X..
- ↑ Smith, Barbara M. (2002). "Principles and Practice of Constraint Programming - CP 2002". 2470. Springer-Verlag. pp. 89–94. doi:10.1007/3-540-46135-3_27..
- ↑ Bosch, Robert; Trick, Michael (2004). "Constraint programming and hybrid formulations for three Life designs". Annals of Operations Research 130 (1–4): 41–56. doi:10.1023/B:ANOR.0000032569.86938.2f..
- ↑ Cheng, Kenil C. K.; Yap, Roland H. C. (2006). "Applying ad-hoc global constraints with the case constraint to still-life". Constraints 11 (2–3): 91–114. doi:10.1007/s10601-006-8058-9..
- ↑ Neil Yorke-Smith. "Maximum Density Still Life". Artificial Intelligence Center. SRI International. http://www.ai.sri.com/~nysmith/life/index.html.
 |