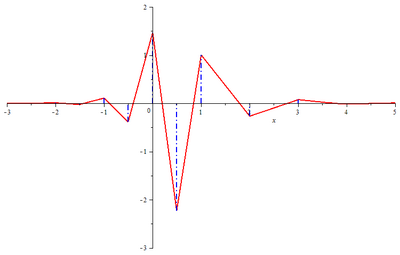
Strömberg wavelet
In mathematics, the Strömberg wavelet is a certain orthonormal wavelet discovered by Jan-Olov Strömberg and presented in a paper published in 1983.[1] Even though the Haar wavelet was earlier known to be an orthonormal wavelet, Strömberg wavelet was the first smooth orthonormal wavelet to be discovered. The term wavelet had not been coined at the time of publishing the discovery of Strömberg wavelet and Strömberg's motivation was to find an orthonormal basis for the Hardy spaces.[1]
Definition
Let m be any non-negative integer. Let V be any discrete subset of the set R of real numbers. Then V splits R into non-overlapping intervals. For any r in V, let Ir denote the interval determined by V with r as the left endpoint. Let P(m)(V) denote the set of all functions f(t) over R satisfying the following conditions:
- f(t) is square integrable.
- f(t) has continuous derivatives of all orders up to m.
- f(t) is a polynomial of degree m + 1 in each of the intervals Ir.
If A0 = {. . . , -2, -3/2, -1, -1/2} ∪ {0} ∪ {1, 2, 3, . . .} and A1 = A0 ∪ { 1/2 } then the Strömberg wavelet of order m is a function Sm(t) satisfying the following conditions:[1]
- [math]\displaystyle{ S^m(t)\in P^{(m)} (A_1). }[/math]
- [math]\displaystyle{ \Vert S^m(t)\Vert=1 }[/math], that is, [math]\displaystyle{ \int_R\vert S^m(t)\vert^2\, dt = 1. }[/math]
- [math]\displaystyle{ S^m(t) }[/math] is orthogonal to [math]\displaystyle{ P^{(m)}(A_0) }[/math], that is, [math]\displaystyle{ \int_R S^m(t)\, f(t)\, dt=0 }[/math] for all [math]\displaystyle{ f(t)\in P^{(m)}(A_0). }[/math]
Properties of the set P(m)(V)
The following are some of the properties of the set P(m)(V):
- Let the number of distinct elements in V be two. Then f(t) ∈ P(m)(V) if and only if f(t) = 0 for all t.
- If the number of elements in V is three or more than P(m)(V) contains nonzero functions.
- If V1 and V2 are discrete subsets of R such that V1 ⊂ V2 then P(m)(V1) ⊂ P(m)(V2). In particular, P(m)(A0) ⊂ P(m)(A1).
- If f(t) ∈ P(m)(A1) then f(t) = g(t) + α λ(t) where α is constant and g(t) ∈ P(m)(A0) is defined by g(r) = f(r) for r ∈ A0.
Strömberg wavelet as an orthonormal wavelet
The following result establishes the Strömberg wavelet as an orthonormal wavelet.[1]
Theorem
Let Sm be the Strömberg wavelet of order m. Then the following set
- [math]\displaystyle{ \left\{2^{j/2}S^m(2^jt-k):j,k \text{ integers }\right\} }[/math]
is a complete orthonormal system in the space of square integrable functions over R.
Strömberg wavelets of order 0
In the special case of Strömberg wavelets of order 0, the following facts may be observed:
- If f(t) ∈ P0(V) then f(t) is defined uniquely by the discrete subset {f(r) : r ∈ V} of R.
- To each s ∈ A0, a special function λs in A0 is associated: It is defined by λs(r) = 1 if r = s and λs(r) = 0 if s ≠ r ∈ A0. These special elements in P(A0) are called simple tents. The special simple tent λ1/2(t) is denoted by λ(t)
Computation of the Strömberg wavelet of order 0
As already observed, the Strömberg wavelet S0(t) is completely determined by the set { S0(r) : r ∈ A1 }. Using the defining properties of the Strömbeg wavelet, exact expressions for elements of this set can be computed and they are given below.[2]
- [math]\displaystyle{ S^0(k) = S^0(1)(\sqrt{3}-2)^{k-1} }[/math] for [math]\displaystyle{ k=1,2,3, \ldots }[/math]
- [math]\displaystyle{ S^0(\tfrac{1}{2}) = -S^0(1)\left(\sqrt{3}+\tfrac{1}{2}\right) }[/math]
- [math]\displaystyle{ S^0(0) = S^0(1)(2\sqrt{3}-2) }[/math]
- [math]\displaystyle{ S^0(-\tfrac{k}{2}) = S^0(1)(2\sqrt{3}-2)(\sqrt{3}-2)^k }[/math] for [math]\displaystyle{ k=1,2,3, \ldots }[/math]
Here S0(1) is constant such that ||S0(t)|| = 1.
Some additional information about Strömberg wavelet of order 0
The Strömberg wavelet of order 0 has the following properties.[2]
- The Strömberg wavelet S0(t) oscillates about t-axis.
- The Strömberg wavelet S0(t) has exponential decay.
- The values of S0(t) for positive integral values of t and for negative half-integral values of t are related as follows: [math]\displaystyle{ S^0(-k/2)=(10-6\sqrt{3})S^0(k) }[/math] for [math]\displaystyle{ k=1,2,3,\ldots\,. }[/math]
References
- ↑ 1.0 1.1 1.2 1.3 Janos-Olov Strömberg, A modified Franklin system and higher order spline systems on Rn as unconditional bases for Hardy spaces, Conference on Harmonic Analysis in Honor of A. Zygmond, Vol. II, W. Beckner, et al (eds.) Wadsworth, 1983, pp.475-494
- ↑ 2.0 2.1 P. Wojtaszczyk (1997). A Mathematical Introduction to Wavelets. Cambridge University Press. pp. 5–14. ISBN 0521570204. https://archive.org/details/mathematicalintr00wojt.
 |