Subcoloring

A non-optimal subcoloring with four colors. Merging the red and blue colors, and the green and yellow colors, produces a subcoloring with only two colors.

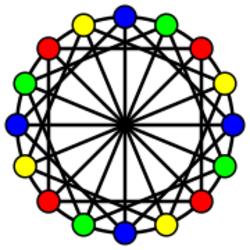
In graph theory, a subcoloring is an assignment of colors to a graph's vertices such that each color class induces a vertex disjoint union of cliques. That is, each color class should form a cluster graph.

The subchromatic number χ_S(G) of a graph G is the fewest colors needed in any subcoloring of G.

Subcoloring and subchromatic number were introduced by (Albertson Jamison).

Every proper coloring and cocoloring of a graph are also subcolorings, so the subchromatic number of any graph is at most equal to the cochromatic number, which is at most equal to the chromatic number.

Subcoloring is as difficult to solve exactly as coloring, in the sense that (like coloring) it is NP-complete. More specifically, the problem of determining whether a planar graph has subchromatic number at most 2 is NP-complete, even if it is a

• triangle-free graph with maximum degree 4 (Gimbel Hartman) (Fiala Klaus),
• comparability graph with maximum degree 4 (Ochem 2017),
• line graph of a bipartite graph with maximum degree 4 (Gonçalves Ochem),
• graph with girth 5 (Montassier Ochem).

The subchromatic number of a cograph can be computed in polynomial time (Fiala Klaus). For every fixed integer r, it is possible to decide in polynomial time whether the subchromatic number of interval and permutation graphs is at most r (Broersma Fomin).

References

• Albertson, M. O.; Jamison, R. E.; Hedetniemi, S. T.; Locke, S. C. (1989), "The subchromatic number of a graph", Discrete Mathematics 74 (1–2): 33–49, doi:10.1016/0012-365X(89)90196-9 .
• Broersma, Hajo; Fomin, Fedor V.; Nesetril, Jaroslav; Woeginger, Gerhard (2002), "More About Subcolorings", Computing 69 (3): 187–203, doi:10.1007/s00607-002-1461-1 .
• Fiala, J.; Klaus, J.; Le, V. B.; Seidel, E. (2003), "Graph Subcolorings: Complexity and Algorithms", SIAM Journal on Discrete Mathematics 16 (4): 635–650, doi:10.1137/S0895480101395245 .
• Gimbel, John; Hartman, Chris (2003), "Subcolorings and the subchromatic number of a graph", Discrete Mathematics 272 (2–3): 139–154, doi:10.1016/S0012-365X(03)00177-8 .
• Gonçalves, Daniel; Ochem, Pascal (2009), "On star and caterpillar arboricity", Discrete Mathematics 309 (11): 3694–3702, doi:10.1016/j.disc.2008.01.041 .
• Montassier, Mickael; Ochem, Pascal (2015), "Near-Colorings: Non-Colorable Graphs and NP-Completeness", Electronic Journal of Combinatorics 22 (1): #P1.57, doi:10.37236/3509, http://www.combinatorics.org/ojs/index.php/eljc/article/view/v22i1p57 .
• Ochem, Pascal (2017), "2-subcoloring is NP-complete for planar comparability graphs", Information Processing Letters 128: 46–48, doi:10.1016/j.ipl.2017.08.004 .