A syntractrix is a curve of the form
- [math]\displaystyle{ x+\sqrt{b^2-y^2}= a \ln \frac{b+\sqrt{b^2-y^2}}{y}. }[/math][1]
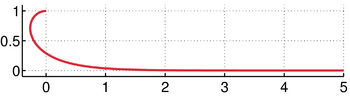
The syntractrix for
[math]\displaystyle{ a=0.5 }[/math] and
[math]\displaystyle{ b=1. }[/math]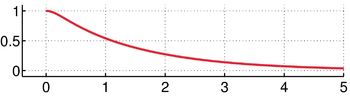
The syntractrix for
[math]\displaystyle{ a=1.5 }[/math] and
[math]\displaystyle{ b=1. }[/math]It is the locus of a point on the tangent of a tractrix at a constant distance from the point of tangency, as the point of tangency is moved along the curve.[2]
References
- ↑ George Salmon (1879). A Treatise on the Higher Plane Curves: Intended as a Sequel to A Treatise on Conic Sections. Published by Hodges, Foster, and Figgis. Page 290. [1]
- ↑ Dionysius Lardner, A system of algebraic geometry 1823, p. 261–263 [2]
 | Original source: https://en.wikipedia.org/wiki/Syntractrix. Read more |




