Tractrix

From HandWiki
Short description: Curve traced by a point on a rod as one end is dragged along a line
Tractrix created by the end of a pole (lying flat on the ground). Its other end is first pushed then dragged by a finger as it spins out to one side.

In geometry, a tractrix (from la trahere 'to pull, drag'; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point (the tractor) that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Isaac Newton (1676) and Christiaan Huygens (1693).[1]

Mathematical derivation

Tractrix with object initially at (4, 0)

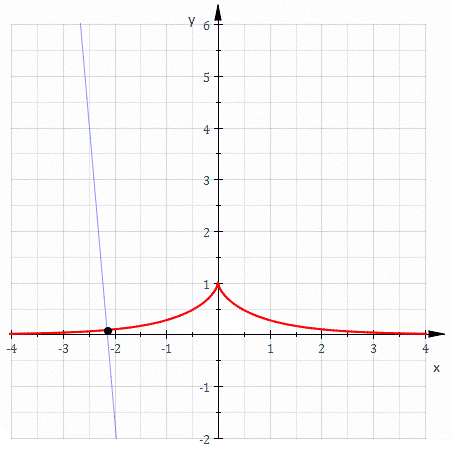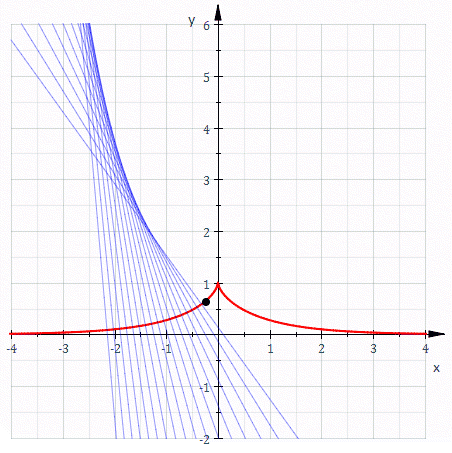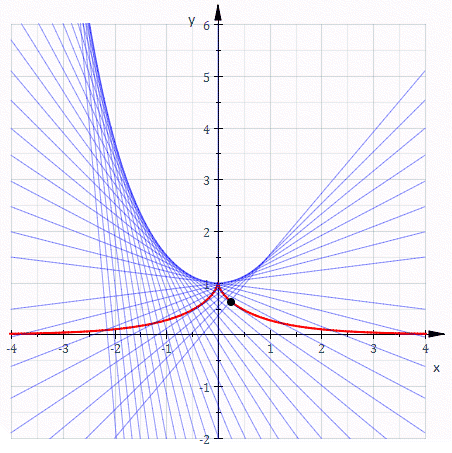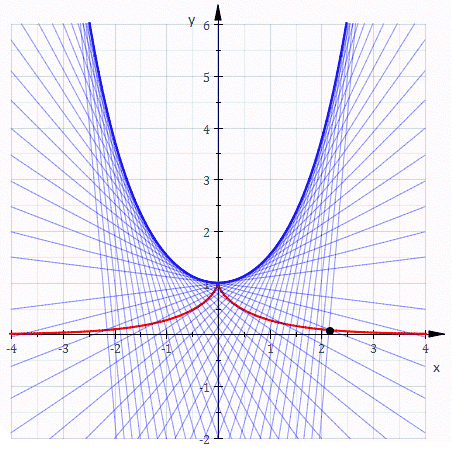
Suppose the object is placed at (a, 0) (or (4, 0) in the example shown at right), and the puller at the origin, so a is the length of the pulling thread (4 in the example at right). Then the puller starts to move along the y axis in the positive direction. At every moment, the thread will be tangent to the curve y = y(x) described by the object, so that it becomes completely determined by the movement of the puller. Mathematically, if the coordinates of the object are (x, y), the y-coordinate of the puller is [math]\displaystyle{ y + \operatorname{sign}(y)\sqrt{a^2 - x^2}, }[/math] by the Pythagorean theorem. Writing that the slope of thread equals that of the tangent to the curve leads to the differential equation

[math]\displaystyle{ \frac{dy}{dx} = \pm\frac{\sqrt{a^2-x^2}}{x} }[/math]

with the initial condition y(a) = 0. Its solution is

[math]\displaystyle{ y = \int_x^a \frac{\sqrt{a^2-t^2}}{t}\,dt = \pm\! \left( a\ln{\frac{a+\sqrt{a^2-x^2}}{x}}-\sqrt{a^2-x^2} \right), }[/math]

where the sign ± depends on the direction (positive or negative) of the movement of the puller.

The first term of this solution can also be written

[math]\displaystyle{ a \operatorname{arsech}\frac{x}{a}, }[/math]

where arsech is the inverse hyperbolic secant function.

The sign before the solution depends whether the puller moves upward or downward. Both branches belong to the tractrix, meeting at the cusp point (a, 0).

Basis of the tractrix

The essential property of the tractrix is constancy of the distance between a point P on the curve and the intersection of the tangent line at P with the asymptote of the curve.

The tractrix might be regarded in a multitude of ways:

  1. It is the locus of the center of a hyperbolic spiral rolling (without skidding) on a straight line.
  2. It is the involute of the catenary function, which describes a fully flexible, inelastic, homogeneous string attached to two points that is subjected to a gravitational field. The catenary has the equation y(x) = a cosh x/a.
  3. The trajectory determined by the middle of the back axle of a car pulled by a rope at a constant speed and with a constant direction (initially perpendicular to the vehicle).
  4. It is a (non-linear) curve which a circle of radius a rolling on a straight line, with its center at the x axis, intersects perpendicularly at all times.

The function admits a horizontal asymptote. The curve is symmetrical with respect to the y-axis. The curvature radius is r = a cot x/y.

A great implication that the tractrix had was the study of its surface of revolution about its asymptote: the pseudosphere. Studied by Eugenio Beltrami in 1868,[citation needed] as a surface of constant negative Gaussian curvature, the pseudosphere is a local model of hyperbolic geometry. The idea was carried further by Kasner and Newman in their book Mathematics and the Imagination, where they show a toy train dragging a pocket watch to generate the tractrix.[2]

Properties

Catenary as evolute of a tractrix
  • The curve can be parameterised by the equation [math]\displaystyle{ x = t - \tanh(t), y= 1/{\cosh(t)} }[/math].[3]
  • Due to the geometrical way it was defined, the tractrix has the property that the segment of its tangent, between the asymptote and the point of tangency, has constant length a.
  • The arc length of one branch between x = x1 and x = x2 is a ln x1/x2.
  • The area between the tractrix and its asymptote is π a2/2, which can be found using integration or Mamikon's theorem.
  • The envelope of the normals of the tractrix (that is, the evolute of the tractrix) is the catenary (or chain curve) given by y = a cosh x/a.
  • The surface of revolution created by revolving a tractrix about its asymptote is a pseudosphere.
  • The tractrix is a transcendental curve; it cannot be defined by a polynomial equation.

Practical application

In 1927, P. G. A. H. Voigt patented a horn loudspeaker design based on the assumption that a wave front traveling through the horn is spherical of a constant radius. The idea is to minimize distortion caused by internal reflection of sound within the horn. The resulting shape is the surface of revolution of a tractrix.[4]
An important application is in the forming technology for sheet metal. In particular a tractrix profile is used for the corner of the die on which the sheet metal is bent during deep drawing.[5]

A toothed belt-pulley design provides improved efficiency for mechanical power transmission using a tractrix catenary shape for its teeth.[6] This shape minimizes the friction of the belt teeth engaging the pulley, because the moving teeth engage and disengage with minimal sliding contact. Original timing belt designs used simpler trapezoidal or circular tooth shapes, which cause significant sliding and friction.

Drawing machines

  • In October–November 1692, Christiaan Huygens described three tractrix-drawing machines.[7]
  • In 1693 Gottfried Wilhelm Leibniz devised a "universal tractional machine" which, in theory, could integrate any first order differential equation.[8] The concept was an analog computing mechanism implementing the tractional principle. The device was impractical to build with the technology of Leibniz's time, and was never realized.
  • In 1706 John Perks built a tractional machine in order to realise the hyperbolic quadrature.[9]
  • In 1729 Giovanni Poleni built a tractional device that enabled logarithmic functions to be drawn.[10]

A history of all these machines can be seen in an article by H. J. M. Bos.[7]

See also

Notes

  1. ↑ Stillwell, John (2010). Mathematics and Its History (revised, 3rd ed.). Springer Science & Business Media. p. 345. ISBN 978-1-4419-6052-8. https://books.google.com/books?id=V7mxZqjs5yUC. , extract of page 345
  2. ↑ Kasner, Edward; Newman, James (2013). "Figure 45(a)". Mathematics and the Imagination. Dover Books on Mathematics. Courier Corporation. p. 141. ISBN 9780486320274. https://books.google.com/books?id=-bXDAgAAQBAJ&pg=PA141. 
  3. ↑ O'Connor, John J.; Robertson, Edmund F., "Tractrix", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Curves/Tractrix.html .
  4. ↑ Horn loudspeaker design pp. 4–5. (Reprinted from Wireless World, March 1974)
  5. ↑ Lange, Kurt (1985). Handbook of Metal Forming. McGraw Hill Book Company. pp. 20.43. 
  6. ↑ "Gates Powergrip GT3 Drive Design Manual". 2014. p. 177. https://www.gates.com/~/media/files/gates/industrial/power-transmission/manuals/powergripdrivedesignmanual_17195_2014.pdf. "The GT tooth profile is based on the tractix mathematical function. Engineering handbooks describe this function as a “frictionless” system. This early development by Schiele is described as an involute form of a catenary." 
  7. ↑ 7.0 7.1 Bos, H. J. M. (1989). "Recognition and Wonder – Huygens, Tractional Motion and Some Thoughts on the History of Mathematics". Euclides 63: 65–76. http://www.gewina.nl/journals/tractrix/bos89.pdf. 
  8. ↑ Milici, Pietro (2014). Lolli, Gabriele. ed. From Logic to Practice: Italian Studies in the Philosophy of Mathematics. Springer. "... mechanical devices studied ... to solve particular differential equations ... We must recollect Leibniz's 'universal tractional machine'" 
  9. ↑ Perks, John (1706). "The construction and properties of a new quadratrix to the hyperbola". Philosophical Transactions 25: 2253–2262. doi:10.1098/rstl.1706.0017. 
  10. ↑ Poleni, John (1729). Epistolarum mathematicanim fasciculus. p. letter no. 7. 

References

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Tractrix&oldid=3380866"