Telephone number (mathematics)

Short description: Number of ways to pair up n objects

The complete graph K₄ has ten matchings, corresponding to the value T(4) = 10 of the fourth telephone number.

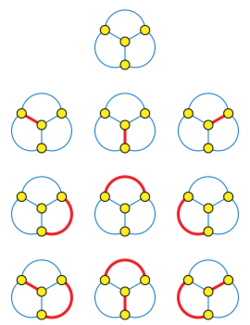
In mathematics, the telephone numbers or the involution numbers form a sequence of integers that count the ways n people can be connected by person-to-person telephone calls. These numbers also describe the number of matchings (the Hosoya index) of a complete graph on n vertices, the number of permutations on n elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with n cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values (starting from n = 0)

1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496, ... (sequence A000085 in the OEIS).

Applications

John Riordan provides the following explanation for these numbers: suppose that n people subscribe to a telephone service that can connect any two of them by a call, but cannot make a single call connecting more than two people. How many different patterns of connection are possible? For instance, with three subscribers, there are three ways of forming a single telephone call, and one additional pattern in which no calls are being made, for a total of four patterns. For this reason, the numbers counting how many patterns are possible are sometimes called the telephone numbers.

Every pattern of pairwise connections between n people defines an involution, a permutation of the people that is its own inverse. In this permutation, each two people who call each other are swapped, and the people not involved in calls remain fixed in place. Conversely, every possible involution has the form of a set of pairwise swaps of this type. Therefore, the telephone numbers also count involutions. The problem of counting involutions was the original combinatorial enumeration problem studied by Rothe in 1800 and these numbers have also been called involution numbers.

In graph theory, a subset of the edges of a graph that touches each vertex at most once is called a matching. Counting the matchings of a given graph is important in chemical graph theory, where the graphs model molecules and the number of matchings is the Hosoya index. The largest possible Hosoya index of an n-vertex graph is given by the complete graphs, for which any pattern of pairwise connections is possible; thus, the Hosoya index of a complete graph on n vertices is the same as the nth telephone number.

A standard Young tableau

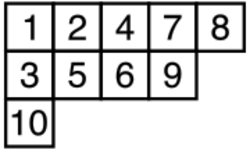
A Ferrers diagram is a geometric shape formed by a collection of n squares in the plane, grouped into a polyomino with a horizontal top edge, a vertical left edge, and a single monotonic chain of edges from top right to bottom left. A standard Young tableau is formed by placing the numbers from 1 to n into these squares in such a way that the numbers increase from left to right and from top to bottom throughout the tableau. According to the Robinson–Schensted correspondence, permutations correspond one-for-one with ordered pairs of standard Young tableaux. Inverting a permutation corresponds to swapping the two tableaux, and so the self-inverse permutations correspond to single tableaux, paired with themselves. Thus, the telephone numbers also count the number of Young tableaux with n squares. In representation theory, the Ferrers diagrams correspond to the irreducible representations of the symmetric group of permutations, and the Young tableaux with a given shape form a basis of the irreducible representation with that shape. Therefore, the telephone numbers give the sum of the degrees of the irreducible representations.

In the mathematics of chess, the telephone numbers count the number of ways to place n rooks on an n × n chessboard in such a way that no two rooks attack each other (the so-called eight rooks puzzle), and in such a way that the configuration of the rooks is symmetric under a diagonal reflection of the board. Via the Pólya enumeration theorem, these numbers form one of the key components of a formula for the overall number of "essentially different" configurations of n mutually non-attacking rooks, where two configurations are counted as essentially different if there is no symmetry of the board that takes one into the other.

Mathematical properties

Recurrence

The telephone numbers satisfy the recurrence relation [math]\displaystyle{ T(n) = T(n-1) + (n-1)T(n-2), }[/math] first published in 1800 by Heinrich August Rothe, by which they may easily be calculated. One way to explain this recurrence is to partition the T(n) connection patterns of the n subscribers to a telephone system into the patterns in which the first person is not calling anyone else, and the patterns in which the first person is making a call. There are T(n − 1) connection patterns in which the first person is disconnected, explaining the first term of the recurrence. If the first person is connected to someone, there are n − 1 choices for that person, and T(n − 2) patterns of connection for the remaining n − 2 people, explaining the second term of the recurrence.

Summation formula and approximation

The telephone numbers may be expressed exactly as a summation [math]\displaystyle{ T(n) = \sum_{k=0}^{\lfloor n/2\rfloor}\binom{n}{2k}(2k-1)!! = \sum_{k=0}^{\lfloor n/2\rfloor}\frac{n!}{2^k (n-2k)! k!}. }[/math] In each term of the first sum, [math]\displaystyle{ k }[/math] gives the number of matched pairs, the binomial coefficient [math]\displaystyle{ \tbinom{n}{2k} }[/math] counts the number of ways of choosing the [math]\displaystyle{ 2k }[/math] elements to be matched, and the double factorial [math]\displaystyle{ (2k-1)!!=\frac{(2k)!}{2^k\,k!} }[/math] is the product of the odd integers up to its argument and counts the number of ways of completely matching the 2k selected elements. It follows from the summation formula and Stirling's approximation that, asymptotically, [math]\displaystyle{ T(n) \sim \left(\frac{n}{e}\right)^{n/2} \frac{e^{\sqrt{n}}}{(4e)^{1/4}}\,. }[/math]

Generating function

The exponential generating function of the telephone numbers is [math]\displaystyle{ \sum_{n=0}^{\infty}\frac{T(n)x^n}{n!}=\exp\left(\frac{x^2}{2}+x\right). }[/math] In other words, the telephone numbers may be read off as the coefficients of the Taylor series of exp(x²/2 + x), and the nth telephone number is the value at zero of the nth derivative of this function. This function is closely related to the exponential generating function of the Hermite polynomials, which are the matching polynomials of the complete graphs. The sum of absolute values of the coefficients of the nth (probabilist's) Hermite polynomial is the nth telephone number, and the telephone numbers can also be realized as certain special values of the Hermite polynomials: [math]\displaystyle{ T(n)=\frac{\mathit{He}_n(i)}{i^n}. }[/math]

Prime factors

For large values of n, the nth telephone number is divisible by a large power of two, 2^{n/4 + O(1)}. More precisely, the 2-adic order (the number of factors of two in the prime factorization) of T(4k) and of T(4k + 1) is k; for T(4k + 2) it is k + 1, and for T(4k + 3) it is k + 2.

For any prime number p, one can test whether there exists a telephone number divisible by p by computing the recurrence for the sequence of telephone numbers, modulo p, until either reaching zero or detecting a cycle. The primes that divide at least one telephone number are

2, 5, 13, 19, 23, 29, 31, 43, 53, 59, ... (sequence A264737 in the OEIS)

The odd primes in this sequence have been called inefficient. Each of them divides infinitely many telephone numbers.