Ternary operation
In mathematics, a ternary operation is an n-ary operation with n = 3. A ternary operation on a set A takes any given three elements of A and combines them to form a single element of A.
In computer science, a ternary operator is an operator that takes three arguments as input and returns one output.[1]
Examples
The function [math]\displaystyle{ T(a, b, c) = ab + c }[/math] is an example of a ternary operation on the integers (or on any structure where [math]\displaystyle{ + }[/math] and [math]\displaystyle{ \times }[/math] are both defined). Properties of this ternary operation have been used to define planar ternary rings in the foundations of projective geometry.
In the Euclidean plane with points a, b, c referred to an origin, the ternary operation [math]\displaystyle{ [a, b, c] = a - b + c }[/math] has been used to define free vectors.[2] Since (abc) = d implies a – b = c – d, these directed segments are equipollent and are associated with the same free vector. Any three points in the plane a, b, c thus determine a parallelogram with d at the fourth vertex.
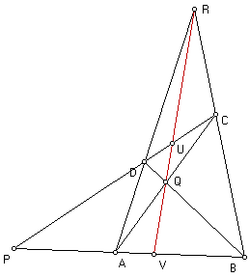
In projective geometry, the process of finding a projective harmonic conjugate is a ternary operation on three points. In the diagram, points A, B and P determine point V, the harmonic conjugate of P with respect to A and B. Point R and the line through P can be selected arbitrarily, determining C and D. Drawing AC and BD produces the intersection Q, and RQ then yields V.
Suppose A and B are given sets and [math]\displaystyle{ \mathcal{B}(A, B) }[/math] is the collection of binary relations between A and B. Composition of relations is always defined when A = B, but otherwise a ternary composition can be defined by [math]\displaystyle{ [p, q, r] = p q^T r }[/math] where [math]\displaystyle{ q^T }[/math] is the converse relation of q. Properties of this ternary relation have been used to set the axioms for a heap.[3]
In Boolean algebra, [math]\displaystyle{ T(A,B,C) = AC+(1-A)B }[/math] defines the formula [math]\displaystyle{ (A \lor B) \land (\lnot A \lor C) }[/math].
Computer science
In computer science, a ternary operator is an operator that takes three arguments (or operands).[1] The arguments and result can be of different types. Many programming languages that use C-like syntax[4] feature a ternary operator, ?:, which defines a conditional expression. In some languages, this operator is referred to as the conditional operator.
In Python, the ternary conditional operator reads x if C else y. Python also supports ternary operations called array slicing, e.g. a[b:c] return an array where the first element is a[b] and last element is a[c-1].[5] OCaml expressions provide ternary operations against records, arrays, and strings: a.[b]<-c would mean the string a where index b has value c.[6]
The multiply–accumulate operation is another ternary operator.
Another example of a ternary operator is between, as used in SQL.
The Icon programming language has a "to-by" ternary operator: the expression 1 to 10 by 2 generates the odd integers from 1 through 9.
In Excel formulae, the form is =if(C, x, y).
See also
- Median algebra or Majority function
- Ternary conditional operator for a list of ternary operators in computer programming languages
- Ternary Exclusive or
- Ternary equivalence relation
References
- ↑ 1.0 1.1 MDN, nmve. "Conditional (ternary) Operator". https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Conditional_Operator. Retrieved 20 February 2017.
- ↑ Jeremiah Certaine (1943) The ternary operation (abc) = a b−1c of a group, Bulletin of the American Mathematical Society 49: 868–77 MR0009953
- ↑ Christopher Hollings (2014) Mathematics across the Iron Curtain: a history of the algebraic theory of semigroups, page 264, History of Mathematics 41, American Mathematical Society ISBN:978-1-4704-1493-1
- ↑ Hoffer, Alex. "Ternary Operator". https://www.cprogramming.com/reference/operators/ternary-operator.html. Retrieved 20 February 2017.
- ↑ "6. Expressions — Python 3.9.1 documentation". https://docs.python.org/3/reference/expressions.html.
- ↑ "The OCaml Manual: Chapter 11 The OCaml language: (7) Expressions". https://v2.ocaml.org/manual/expr.html.
External links
 |  |
