Tomahawk (geometry)

From HandWiki
Short description: Tool for trisecting angles
A tomahawk, with its handle and spike thickened

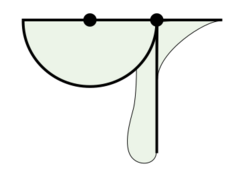
The tomahawk is a tool in geometry for angle trisection, the problem of splitting an angle into three equal parts. The boundaries of its shape include a semicircle and two line segments, arranged in a way that resembles a tomahawk, a Native American axe.[1][2] The same tool has also been called the shoemaker's knife,[3] but that name is more commonly used in geometry to refer to a different shape, the arbelos (a curvilinear triangle bounded by three mutually tangent semicircles).[4]

Description

The basic shape of a tomahawk consists of a semicircle (the "blade" of the tomahawk), with a line segment the length of the radius extending along the same line as the diameter of the semicircle (the tip of which is the "spike" of the tomahawk), and with another line segment of arbitrary length (the "handle" of the tomahawk) perpendicular to the diameter. In order to make it into a physical tool, its handle and spike may be thickened, as long as the line segment along the handle continues to be part of the boundary of the shape. Unlike a related trisection using a carpenter's square, the other side of the thickened handle does not need to be made parallel to this line segment.[1]

In some sources a full circle rather than a semicircle is used,[5] or the tomahawk is also thickened along the diameter of its semicircle,[6] but these modifications make no difference to the action of the tomahawk as a trisector.

Trisection

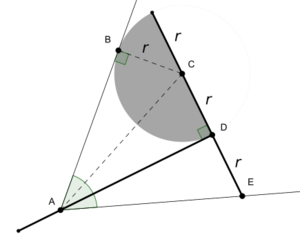
A tomahawk trisecting an angle. The handle AD forms one trisector and the dotted line AC to the center of the semicircle forms the other.

To use the tomahawk to trisect an angle, it is placed with its handle line touching the apex of the angle, with the blade inside the angle, tangent to one of the two rays forming the angle, and with the spike touching the other ray of the angle. One of the two trisecting lines then lies on the handle segment, and the other passes through the center point of the semicircle.[1][6] If the angle to be trisected is too sharp relative to the length of the tomahawk's handle, it may not be possible to fit the tomahawk into the angle in this way, but this difficulty may be worked around by repeatedly doubling the angle until it is large enough for the tomahawk to trisect it, and then repeatedly bisecting the trisected angle the same number of times as the original angle was doubled.[2]

If the apex of the angle is labeled A, the point of tangency of the blade is B, the center of the semicircle is C, the top of the handle is D, and the spike is E, then triangles △ACD and △ADE are both right triangles with a shared base and equal height, so they are congruent triangles. Because the sides AB and BC of triangle △ABC are respectively a tangent and a radius of the semicircle, they are at right angles to each other and △ABC is also a right triangle; it has the same hypotenuse as △ACD and the same side lengths BC = CD, so again it is congruent to the other two triangles, showing that the three angles formed at the apex are equal.[5][6]

Although the tomahawk may itself be constructed using a compass and straightedge,[7] and may be used to trisect an angle, it does not contradict Pierre Wantzel's 1837 theorem that arbitrary angles cannot be trisected by compass and unmarked straightedge alone.[8] The reason for this is that placing the constructed tomahawk into the required position is a form of neusis that is not allowed in compass and straightedge constructions.[9]

History

The inventor of the tomahawk is unknown,[1][10] but the earliest references to it come from 19th-century France. It dates back at least as far as 1835, when it appeared in a book by Claude Lucien Bergery, Géométrie appliquée à l'industrie, à l'usage des artistes et des ouvriers (3rd edition).[1] Another early publication of the same trisection was made by Henri Brocard in 1877;[11] Brocard in turn attributes its invention to an 1863 memoir by French naval officer Pierre-Joseph Glotin (d).[12][13][14]

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 Yates, Robert C. (1941), "The Trisection Problem, Chapter III: Mechanical trisectors", National Mathematics Magazine 15 (6): 278–293, doi:10.2307/3028413 .
  2. ↑ 2.0 2.1 Gardner, Martin (1975), Mathematical Carnival: from penny puzzles, card shuffles and tricks of lightning calculators to roller coaster rides into the fourth dimension, Knopf, pp. 262–263 .
  3. ↑ Dudley, Underwood (1996), The Trisectors, MAA Spectrum (2nd ed.), Cambridge University Press, pp. 14–16, ISBN 9780883855140 .
  4. ↑ Alsina, Claudi; Nelsen, Roger B. (2010), "9.4 The shoemaker's knife and the salt cellar", Charming Proofs: A Journey Into Elegant Mathematics, Dolciani Mathematical Expositions, 42, Mathematical Association of America, pp. 147–148, ISBN 9780883853481 .
  5. ↑ 5.0 5.1 Meserve, Bruce E. (1982), Fundamental Concepts of Algebra, Courier Dover Publications, p. 244, ISBN 9780486614700, https://books.google.com/books?id=qtuySdnGDtoC&pg=PA244 .
  6. ↑ 6.0 6.1 6.2 Isaacs, I. Martin (2009), Geometry for College Students, Pure and Applied Undergraduate Texts, 8, American Mathematical Society, pp. 209–210, ISBN 9780821847947 .
  7. ↑ Eves, Howard Whitley (1995), College Geometry, Jones & Bartlett Learning, p. 191, ISBN 9780867204759, https://books.google.com/books?id=B81gnTjNazMC&pg=PA191 .
  8. ↑ "Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas" (in French), Journal de Mathématiques Pures et Appliquées 1 (2): 366–372, 1837, http://visualiseur.bnf.fr/ConsulterElementNum?O=NUMM-16381&Deb=374&Fin=380&E=PDF .
  9. ↑ The word "neusis" is described by La Nave, Federica (2002), "Reading Bombelli", The Mathematical Intelligencer 24 (1): 12–21, doi:10.1007/BF03025306  as meaning "a family of constructions dependent upon a single parameter" in which, as the parameter varies, some combinatorial change in the construction occurs at the desired parameter value. La Nave and Mazur describe other trisections than the tomahawk, but the same description applies here: a tomahawk placed with its handle on the apex, parameterized by the position of the spike on its ray, gives a family of constructions in which the relative positions of the blade and its ray change as the spike is placed at the correct point.
  10. ↑ Aaboe, Asger (1997), Episodes from the Early History of Mathematics, New Mathematical Library, 13, Mathematical Association of America, p. 87, ISBN 9780883856130, https://books.google.com/books?id=5wGzF0wPFYgC&pg=PA87 .
  11. ↑ Brocard, H. (1877), "Note sur la division mécanique de l'angle" (in French), Bulletin de la Société Mathématique de France 5: 43–47, http://www.numdam.org/item?id=BSMF_1877__5__43_1 .
  12. ↑ Glotin (1863), "De quelques moyens pratiques de diviser les angles en parties égales" (in French), Mémoires de la Société des Sciences physiques et naturelles de Bordeaux 2: 253–278, https://books.google.com/books?id=FQ9_wRdXYXUC&pg=PA253 .
  13. ↑ George E. Martin (1998), "Preface", Geometric Constructions, Springer, http://math.albany.edu/pers/preface.html 
  14. ↑ (Dudley 1996) incorrectly writes these names as Bricard and Glatin.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Tomahawk_(geometry)&oldid=2998768"