Toom's rule
Toom's rule is a 2-dimensional cellular automaton model created by Andrei Toom in 1978.[1][2] It is a modification of the 2-dimensional majority vote rule and can have more robust memory when considered as a thermal physical system in statistical field theory.[3] The model also has a noise-dependent phase transition.[1]
Statement


Toom's rule is a cellular automaton that acts on a 2-dimensional square lattice. At each site in this lattice is a spin with the value +1 or -1. At time the bits are initialized to some value. At each discrete time step the lattice evolves according to Toom's rule. This rule is applied at each site simultaneously.
A deterministic version of Toom's rule can be stated as:
- At each site in the lattice if the spin of the current (center) site plus the neighboring spin to the North plus the neighboring spin to the East is greater than 0, then the current spin becomes +1 in the next time step.
- If this sum is less than 0, then the current spin becomes -1 in the next time step. As there are 3 spins the sum can never equal 0.
Toom's rule is sometimes called the NEC rule since it involves the North, East, and Center sites.[1]
The general version of Toom's rule is probabilistic and can be stated as:
- Apply the deterministic version of Toom's rule.
- If step 1 results in a spin of +1 change it to -1 with probability q. Otherwise, if step 2 results in a spin of -1 change it to +1 with probability p.[4]
The deterministic version can be recovered by setting p=q=0.
Toom's rule is an example of a probabilistic cellular automata (see Stochastic cellular automaton), defined on the lattice .[1]
Properties
When the system will tend to favor one spin over the other, which can be interpreted as the effect of a magnetic field.[1]
The model has a phase transition. For low enough p, q, there are at least two steady states, but for high enough p, q, there is a unique steady state.[1] This is proven in Toom's original paper.[2]
When p=q=0, there is a steady state with a staircase-like boundary (interface) between +1 and -1 spins. When p, q are small, there are fluctuations along this interface. Additional models have been built to study the interface dynamics as a 1D spin configuration (on ).
One can define as the rate (probability) that each +1 exchanges places with the first -1 spin on its right. The rate can be defined similarly. One can make a further simplification that only the leftmost spin in a block (of identical spins) exchanges places with the first opposite spin to the right. Also, let the first spin flip independently with probability . This 1D model has also been called Toom's rule.[1]
When studying the steady state where
, the density of site n (the expected value of site n) follows the scale law:[1]
One can also define a finite version of this 1D Toom's rule where there are L sites (finite interface model). The leftmost -1 in a block exchanges with the first +1 to the right with probability
, and the leftmost +1 in a block exchanges with the first -1 to the right with probability
. In this model, there are u up spins and d down spins where u+d=L. There are also
configurations of the L sites.[1]
The correlation functions, partition function, Markov Matrices, and their eigenvalues can be computed for this finite Toom rule. It has been shown that when and large n < L, the density function follows the same inverse square law as above: .
When it is conjectured that the density decays like 1/n.[1]
Toom's rule as a memory
Toom's rule is a dynamical variant of the Ising model. There are many dynamical rules for the Ising model where the steady state is Gibbsian.[1]
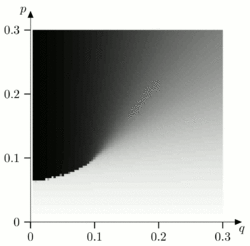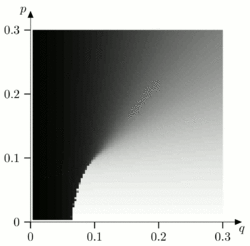

The 2-dimensional ferromagnetic Ising model in the absence of local magnetic fields has two ground states: one with all spins in the lattice having +1 (spin up) and the other with all spins in the lattice having -1 (spin down). For this reason, the 2D Ising model can be seen as a memory storing one bit of information in the ground state.
This memory is robust in the sense that if errors cause some spins to flip, returning to the ground state will preserve the stored information. These errors occur due to thermal noise in the system. Therefore it is said this memory is robust in the presence of thermal noise. However, if there is a local magnetic field which favors one ground state over the other, then the Ising model is no longer a reliable memory since there is only one ground state.
The 2-dimensional majority vote cellular automaton (CA) is analogous to the Ising model. The majority vote CA evolves each site in the lattice by taking the spin value of current site plus that of the 4 neighboring sites and makes this spin +1 in the next time step if the sum is positive and -1 if the sum is negative. Just as for Toom's rule we can construct a probabilistic version of the majority vote CA where the output can be changed with probability q from spin +1 to spin -1 and with probability p from spin -1 to a spin +1.
Instead of ground states, information is stored in stable states of the CA. These are states such that the spins on the lattice do not change when acted upon by the CA. It is easy to show that the all +1 and the all -1 states are stable states when q=p=0. Therefore the majority vote CA can be used to store information. We can define terms analogous to thermal noise and magnetic field as T=p+q and h=(p-q)/(p+q) respectively. Similarly to the Ising model the majority vote CA can reliably store information for small values of T. Unlike the Ising mode, if T is small enough, this is even true for arbitrary values of h.[4][5]
Toom's model can be applied to fault-tolerant computation.[5]
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 Ayyer, Arvind (August 2015). "A finite variant of the Toom Model" (in en). Journal of Physics: Conference Series 638 (1): 012005. doi:10.1088/1742-6596/638/1/012005. ISSN 1742-6596. https://dx.doi.org/10.1088/1742-6596/638/1/012005.
- ↑ 2.0 2.1 Toom, Andrei (1980). "Stable and attractive trajectories in multicomponent systems". Multicomponent Random Systems: 549–575.
- ↑ Bernd Gartner, Ahad N. Zehmakan (2017). "Color War: Cellular Automata with Majority Rule". Lata2017: 393–404.
- ↑ 4.0 4.1 Grinstein, G. (1 January 2004). "Can complex structures be generically stable in a noisy world?". IBM Journal of Research and Development 48 (1): 5–12. doi:10.1147/rd.481.0005.
- ↑ 5.0 5.1 Gacs, Peter. ""A New Version of Toom's Proof“, Technical Report BUCS-1995-009, Computer Science Department, Boston University, March 27, 1995.". Boston University. http://hdl.handle.net/2144/1570. Retrieved 8 April 2020.
 |
