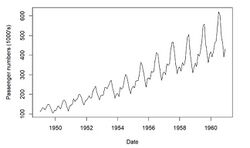
Trend periodic nonstationary processes
Trend periodic non-stationary processes (or trend cyclostationary processes) are a type of cyclostationary process that exhibits both periodic behavior and a statistical trend. The trend can be linear or nonlinear, and it can result from systematic changes in the data over time. A cyclostationary process can be formed by removing the trend component. This approach is utilized in the analysis of the trend-stationary process.
In data analysis classification of periodic data into stationary-periodic, trend-periodic and stochastic-periodic time series is achieved by means of phase dispersion minimization (PDM) test, which is a method for identifying periodicity.[1]
Applications
Trending cyclostationary processes have several applications in finance, engineering, economics, and environmental research. Trending cyclostationary processes are used in economics to predict the seasonality and trend of time series data that display both periodic and trending behavior, such as rail and air travel demand.[2] Trending cyclostationary processes are used in engineering to simulate signals that display both periodic and trending behavior, such as signals in modulated radio communications or control systems.[3] Trending cyclostationary processes are used in economics to represent time series data that display both periodic behavior and trends in which the trend is usually represented by a so-called unit root in the autoregressive part of the model.[4] Trending cyclostationary processes are used in environmental research to simulate time series data that display both periodic behavior and trends, such as temperature or pollutant appearance patterns.[5] In fact, almost any pollutions related phenomena falls into one of stochastic, periodic-stochastic, or trend-period-stochastic processes.[6]
Properties
Trending cyclostationary processes have traits that are a mix of cyclostationary processes and trends. Trending cyclostationary processes have second-order stationarity, which means that their second-order moments are time-periodic. They do, however, display non-stationarity, which means that their mean and variance alter over time as a result of the presence of the trend.
A trend periodic stationary process is a sort of stationary time series data that has a consistent underlying trend that repeats itself regularly. A Fourier series expansion is a popular mathematical depiction of a trend periodic stationary process:
- [math]\displaystyle{ x(t) = a_0 + \sum_{k=1}^\infty(a_k cos(2\pi kt/T) + b_k sin(2\pi kt/T)) }[/math]
where x(t) is the time series data, T is the period of the trend, [math]\displaystyle{ a_0 }[/math] is the mean of the series, [math]\displaystyle{ a_k }[/math] and [math]\displaystyle{ b_k }[/math] are the Fourier coefficients, and k is the harmonic number.
Another way to represent trend periodic stationary processes is by using a regression model with a sine and cosine function, such as:
- [math]\displaystyle{ x(t) = \beta_0 + \beta_1 t+ \beta_2 cos(2 \pi t/T) + \beta_3sin(2\pi t/T) }[/math]
where [math]\displaystyle{ \beta_0 }[/math], [math]\displaystyle{ \beta_1 }[/math], [math]\displaystyle{ \beta_2 }[/math], and [math]\displaystyle{ \beta_3 }[/math] are the regression coefficients that can be estimated using statistical methods.
Decomposing the signal is widely used to separate the trend process from the periodic one and represent the periodic part as sinusoid functions. The spectral density estimation is one of the methods used for this purpose. The decomposed function of the periodic trend process has a trend and a principal function that governs the periodicity.[7]
Example
An example of trend periodic in the second form is [math]\displaystyle{ x(t) = 10 t+ 2 + 5 cos(2 \pi t/10) + 7sin(2\pi t/10) }[/math] where 10t is trend and [math]\displaystyle{ a_0=2 }[/math] plus the sinusiduals are periodic stationary processes.
Detection and estimation
Estimation and detection of trending cyclostationary processes are more difficult than for standard cyclostationary processes due to discrepancies in trend definitions. [8] One popular strategy is to first remove the trend from the data before estimating and detecting cyclostationary processes. Another strategy is to represent the data as a cyclostationary process and a trend and estimate the parameters of both components at the same time.
References
- ↑ Poghosyan, Arnak; Harutyunyan, Ashot; Grigoryan, Naira; Pang, Clement; Oganesyan, George; Ghazaryan, Sirak; Hovhannisyan, Narek (25 February 2021). "An Enterprise Time Series Forecasting System for Cloud Applications Using Transfer Learning". Sensors 21 (1590): 1590. doi:10.3390/s21051590. PMID 33668753. Bibcode: 2021Senso..21.1590P.
- ↑ Proietti, T; Marczak, M; Mazzi, G (2019). "A class of periodic trend models for seasonal time series". Journal of Forecasting 38 (2): 106–121. doi:10.1002/for.2562.
- ↑ Gardner, William A (1994). Cyclostationarity In Communications and Signal Processing. IEEE Press. ISBN 9780780310230.
- ↑ Franses, Philip Hans; Paap, Richard (2004). Periodic Time Series Models. London: Oxford University Press. ISBN 9780199242023.
- ↑ Deshcherevskii, A.V.; Sidorin, A.Y. (2021). "Iterative Algorithm for Time Series Decomposition into Trend and Seasonality: Testing Using the Example of CO2 Concentrations in the Atmosphere". Izv. Atmos. Ocean. Phys. 57 (8): 813–836. doi:10.1134/S0001433821080028. Bibcode: 2021IzAOP..57..813D.
- ↑ Sydow, Achim (2010). Environmental Systems. II. EOLSS Publications.
- ↑ Ogura, H (March 1971). "Spectral representation of a periodic nonstationary random process". IEEE Transactions on Information Theory 17 (2): 143-149. doi:10.1109/TIT.1971.1054612.
- ↑ Wu, Zhaohua; Huang, Norden E.; Long, Steven R.; Peng, Chung-Kang (2007). "On the trend, detrending, and variability of nonlinear and nonstationary time series". Proceedings of the National Academy of Sciences 104 (38): 14889–14894. doi:10.1073/pnas.0701020104. PMID 17846430. Bibcode: 2007PNAS..10414889W.
 |