Triangulated irregular network
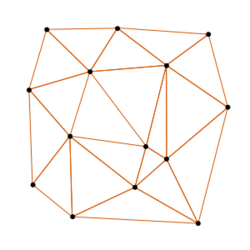
In computer graphics, a triangulated irregular network (TIN)[1] is a representation of a continuous surface consisting entirely of triangular facets (a triangle mesh), used mainly as Discrete Global Grid in primary elevation modeling.
The vertices of these triangles are created from field recorded spot elevations through a variety of means including surveying through conventional techniques, Global Positioning System Real-Time Kinematic (GPS RTK), photogrammetry, or some other means. Associated with three-dimensional [math]\displaystyle{ (x, y, z) }[/math] data and topography, TINs are useful for the description and analysis of general horizontal [math]\displaystyle{ (x, y) }[/math] distributions and relationships.
Digital TIN data structures are used in a variety of applications, including geographic information systems (GIS), and computer aided design (CAD) for the visual representation of a topographical surface. A TIN is a vector-based representation of the physical land surface or sea bottom, made up of irregularly distributed nodes and lines with three-dimensional coordinates [math]\displaystyle{ (x, y, z) }[/math] that are arranged in a network of non-overlapping triangles.
A TIN comprises a triangular network of vertices, known as mass points, with associated coordinates in three dimensions connected by edges to form a triangular tessellation. Three-dimensional visualizations are readily created by rendering of the triangular facets. In regions where there is little variation in surface height, the points may be widely spaced whereas in areas of more intense variation in height the point density is increased.
A TIN used to represent terrain is often called a digital elevation model (DEM), which can be further used to produce digital surface models (DSM) or digital terrain models (DTM). An advantage of using a TIN over a rasterized digital elevation model (DEM) in mapping and analysis is that the points of a TIN are distributed variably based on an algorithm that determines which points are most necessary to create an accurate representation of the terrain. Data input is therefore flexible and fewer points need to be stored than in a raster DEM, with regularly distributed points. While a TIN may be considered less suited than a raster DEM for certain kinds of GIS applications, such as analysis of a surface's slope and aspect, it is often used in CAD to create contour lines. A DTM and DSM can be formed from a DEM. A DEM can be interpolated from a TIN.
TIN are based on a Delaunay triangulation or constrained Delaunay. Delaunay conforming triangulations are recommended over constrained triangulations. This is because the resulting TINs are likely to contain fewer long, skinny triangles, which are undesirable for surface analysis. Additionally, natural neighbor interpolation and Thiessen (Voronoi) polygon generation can only be performed on Delaunay conforming triangulations. A constrained Delaunay triangulation can be considered when you need to explicitly define certain edges that are guaranteed not to be modified (that is, split into multiple edges) by the triangulator. Constrained Delaunay triangulations are also useful for minimizing the size of a TIN, since they have fewer nodes and triangles where breaklines are not densified.
The TIN model was developed in the early 1970s as a simple way to build a surface from a set of irregularly spaced points. The first triangulated irregular network program for GIS was written by W. Randolph Franklin, under the direction of David Douglas and Thomas Peucker (Poiker), at Simon Fraser University in 1973.[2]
File formats
A variety of different file formats exist for saving TIN information, including Esri TIN, along with others such as AquaVeo[3] and ICEM CFD.[4]
References
- ↑ [1]Also known as a "Triangular Irregular Network"
- ↑ Franklin, W. R. (1973). Triangulated irregular network program.
- ↑ "TIN Files - XMS Wiki". https://www.xmswiki.com/wiki/TIN_Files.
- ↑ "[ICEM] Import geometry from solidworks -- CFD Online Discussion Forums". https://www.cfd-online.com/Forums/ansys-meshing/71507-import-geometry-solidworks.html.
External links
 |  |
