Truncus (mathematics)

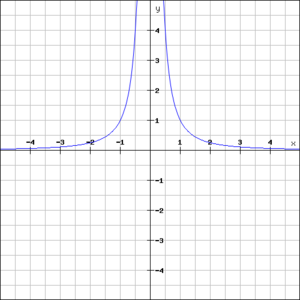
In analytic geometry, a truncus is a curve in the Cartesian plane consisting of all points (x,y) satisfying an equation of the form

A mathematical graph of the basic truncus forumula, marked in blue, with domain and range both restricted to [-5, 5].

[math]\displaystyle{ f(x) = {a \over (x + b)^2} + c }[/math]

where a, b, and c are given constants. The two asymptotes of a truncus are parallel to the coordinate axes. The basic truncus y = 1 / x² has asymptotes at x = 0 and y = 0, and every other truncus can be obtained from this one through a combination of translations and dilations.

For the general truncus form above, the constant a dilates the graph by a factor of a from the x-axis; that is, the graph is stretched vertically when a > 1 and compressed vertically when 0 < a < 1. When a < 0 the graph is reflected in the x-axis as well as being stretched vertically. The constant b translates the graph horizontally left b units when b > 0, or right when b < 0. The constant c translates the graph vertically up c units when c > 0 or down when c < 0. The asymptotes of a truncus are found at x = -b (for the vertical asymptote) and y = c (for the horizontal asymptote).