Trémaux tree
In graph theory, a Trémaux tree of an undirected graph [math]\displaystyle{ G }[/math] is a type of spanning tree, generalizing depth-first search trees. They are defined by the property that every edge of [math]\displaystyle{ G }[/math] connects an ancestor–descendant pair in the tree. Trémaux trees are named after Charles Pierre Trémaux, a 19th-century French author who used a form of depth-first search as a strategy for solving mazes.[1][2] They have also been called normal spanning trees, especially in the context of infinite graphs.[3][4]
All depth-first search trees and all Hamiltonian paths are Trémaux trees. In finite graphs, every Trémaux tree is a depth-first search tree, but although depth-first search itself is inherently sequential, Trémaux trees can be constructed by a randomized parallel algorithm in the complexity class RNC. They can be used to define the tree-depth of a graph, and as part of the left-right planarity test for testing whether a graph is a planar graph. A characterization of Trémaux trees in the monadic second-order logic of graphs allows graph properties involving orientations to be recognized efficiently for graphs of bounded treewidth using Courcelle's theorem.
Not every infinite connected graph has a Trémaux tree, and not every infinite Trémaux tree is a depth-first search tree. The graphs that have Trémaux trees can be characterized by forbidden minors. An infinite Trémaux tree must have exactly one infinite path for each end of the graph, and the existence of a Trémaux tree characterizes the graphs whose topological completions, formed by adding a point at infinity for each end, are metric spaces.
Definition and examples
A Trémaux tree, for a graph [math]\displaystyle{ G }[/math], is a spanning tree [math]\displaystyle{ T }[/math] with the property that, for every edge [math]\displaystyle{ uv }[/math] in [math]\displaystyle{ G }[/math], one of the two endpoints [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] is an ancestor of the other. To be a spanning tree, it must only use edges of [math]\displaystyle{ G }[/math], and include every vertex, with a unique finite path between every pair of vertices. Additionally, to define the ancestor–descendant relation in this tree, one of its vertices must be designated as its root.
If a finite graph has a Hamiltonian path, then rooting that path at one of its two endpoints produces a Trémaux tree. For such a path, every pair of vertices is an ancestor–descendant pair.
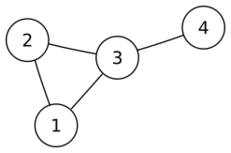
In the graph shown below, the tree with edges 1–3, 2–3, and 3–4 is a Trémaux tree when it is rooted at vertex 1 or vertex 2: every edge of the graph belongs to the tree except for the edge 1–2, which (for these choices of root) connects an ancestor-descendant pair.
However, rooting the same tree at vertex 3 or vertex 4 produces a rooted tree that is not a Trémaux tree, because with this root 1 and 2 are no longer an ancestor and descendant of each other.
In finite graphs
Existence
Every finite connected undirected graph has at least one Trémaux tree.[4] One can construct such a tree by performing a depth-first search and connecting each vertex (other than the starting vertex of the search) to the earlier vertex from which it was discovered. The tree constructed in this way is known as a depth-first search tree. If [math]\displaystyle{ uv }[/math] is an arbitrary edge in the graph, and [math]\displaystyle{ u }[/math] is the earlier of the two vertices to be reached by the search, then [math]\displaystyle{ v }[/math] must belong to the subtree descending from [math]\displaystyle{ u }[/math] in the depth-first search tree, because the search will necessarily discover [math]\displaystyle{ v }[/math] while it is exploring this subtree, either from one of the other vertices in the subtree or, failing that, from [math]\displaystyle{ u }[/math] directly. Every finite Trémaux tree can be generated as a depth-first search tree: If [math]\displaystyle{ T }[/math] is a Trémaux tree of a finite graph, and a depth-first search explores the children in [math]\displaystyle{ T }[/math] of each vertex prior to exploring any other vertices, it will necessarily generate [math]\displaystyle{ T }[/math] as its depth-first search tree.
Parallel construction
| Unsolved problem in computer science: Is there a deterministic parallel NC algorithm for constructing Trémaux trees? (more unsolved problems in computer science)
|
It is P-complete to find the Trémaux tree that would be found by a sequential depth-first search algorithm, in which the neighbors of each vertex are searched in order by their identities.[5] Nevertheless, it is possible to find a different Trémaux tree by a randomized parallel algorithm, showing that the construction of Trémaux trees belongs to the complexity class RNC. The algorithm is based on another randomized parallel algorithm, for finding minimum-weight perfect matchings in 0-1-weighted graphs.[6] As of 1997, it remained unknown whether Trémaux tree construction could be performed by a deterministic parallel algorithm, in the complexity class NC.[7] If matchings can be found in NC, then so can Trémaux trees.[6]
Logical expression
It is possible to express the property that a set [math]\displaystyle{ T }[/math] of edges with a choice of root vertex [math]\displaystyle{ r }[/math] forms a Trémaux tree, in the monadic second-order logic of graphs, and more specifically in the form of this logic called MSO2, which allows quantification over both vertex and edge sets. This property can be expressed as the conjunction of the following properties:
- The graph is connected by the edges in [math]\displaystyle{ T }[/math]. This can be expressed logically as the statement that, for every non-empty proper subset of the graph's vertices, there exists an edge in [math]\displaystyle{ T }[/math] with exactly one endpoint in the given subset.
- [math]\displaystyle{ T }[/math] is acyclic. This can be expressed logically as the statement that there does not exist a nonempty subset [math]\displaystyle{ C }[/math] of [math]\displaystyle{ T }[/math] for which each vertex is incident to either zero or two edges of [math]\displaystyle{ C }[/math].
- Every edge [math]\displaystyle{ e }[/math] not in [math]\displaystyle{ T }[/math] connects an ancestor-descendant pair of vertices in [math]\displaystyle{ T }[/math]. This is true when both endpoints of [math]\displaystyle{ e }[/math] belong to a path in [math]\displaystyle{ T }[/math]. It can be expressed logically as the statement that, for all edges [math]\displaystyle{ e }[/math], there exists a subset [math]\displaystyle{ P }[/math] of [math]\displaystyle{ T }[/math] such that exactly two vertices, one of them [math]\displaystyle{ r }[/math], are incident to a single edge of [math]\displaystyle{ P }[/math], and such that both endpoints of [math]\displaystyle{ e }[/math] are incident to at least one edge of [math]\displaystyle{ P }[/math].
Once a Trémaux tree has been identified in this way, one can describe an orientation of the given graph, also in monadic second-order logic, by specifying the set of edges whose orientation is from the ancestral endpoint to the descendant endpoint. The remaining edges outside this set must be oriented in the other direction. This technique allows graph properties involving orientations to be specified in monadic second order logic, allowing these properties to be tested efficiently on graphs of bounded treewidth using Courcelle's theorem.[8]
Related properties
If a graph has a Hamiltonian path, then that path (rooted at one of its endpoints) is also a Trémaux tree. The undirected graphs for which every Trémaux tree has this form are the cycle graphs, complete graphs, and balanced complete bipartite graphs.[9]
Trémaux trees are closely related to the concept of tree-depth. The tree-depth of a graph [math]\displaystyle{ G }[/math] can be defined as the smallest number [math]\displaystyle{ d }[/math] for which there exist a graph [math]\displaystyle{ H }[/math], with a Trémaux tree [math]\displaystyle{ T }[/math] of depth [math]\displaystyle{ d }[/math], such that [math]\displaystyle{ G }[/math] is a subgraph of [math]\displaystyle{ H }[/math]. Bounded tree-depth, in a family of graphs, is equivalent to the existence of a path that cannot occur as a graph minor of the graphs in the family. Many hard computational problems on graphs have algorithms that are fixed-parameter tractable when parameterized by the tree-depth of their inputs.[10]
Trémaux trees also play a key role in the Fraysseix–Rosenstiehl planarity criterion for testing whether a given graph is planar. According to this criterion, a graph [math]\displaystyle{ G }[/math] is planar if, for a given Trémaux tree [math]\displaystyle{ T }[/math] of [math]\displaystyle{ G }[/math], the remaining edges can be placed in a consistent way to the left or the right of the tree, subject to constraints that prevent edges with the same placement from crossing each other.[11]
In infinite graphs
Existence
Not every infinite graph has a normal spanning tree. For instance, a complete graph on an uncountable set of vertices does not have one: a normal spanning tree in a complete graph can only be a path, but a path has only a countable number of vertices. However, every graph on a countable set of vertices does have a normal spanning tree.[3][4]
Even in countable graphs, a depth-first search might not succeed in eventually exploring the entire graph,[3] and not every normal spanning tree can be generated by a depth-first search: to be a depth-first search tree, a countable normal spanning tree must have only one infinite path or one node with infinitely many children (and not both).
Minors
If an infinite graph [math]\displaystyle{ G }[/math] has a normal spanning tree, so does every connected graph minor of [math]\displaystyle{ G }[/math]. It follows from this that the graphs that have normal spanning trees have a characterization by forbidden minors. One of the two classes of forbidden minors consists of bipartite graphs in which one side of the bipartition is countable, the other side is uncountable, and every vertex has infinite degree. The other class of forbidden minors consists of certain graphs derived from Aronszajn trees.[12]
The details of this characterization depend on the choice of set-theoretic axiomatization used to formalize mathematics. In particular, in models of set theory for which Martin's axiom is true and the continuum hypothesis is false, the class of bipartite graphs in this characterization can be replaced by a single forbidden minor. However, for models in which the continuum hypothesis is true, this class contains graphs which are incomparable with each other in the minor ordering.[13]
Ends and metrizability
Normal spanning trees are also closely related to the ends of an infinite graph, equivalence classes of infinite paths that, intuitively, go to infinity in the same direction. If a graph has a normal spanning tree, this tree must have exactly one infinite path for each of the graph's ends.[14]
An infinite graph can be used to form a topological space by viewing the graph itself as a simplicial complex and adding a point at infinity for each end of the graph. With this topology, a graph has a normal spanning tree if and only if its set of vertices can be decomposed into a countable union of closed sets. Additionally, this topological space can be represented by a metric space if and only if the graph has a normal spanning tree.[14]
References
- ↑ Even, Shimon (2011), Graph Algorithms (2nd ed.), Cambridge University Press, pp. 46–48, ISBN 978-0-521-73653-4, https://books.google.com/books?id=m3QTSMYm5rkC&pg=PA46.
- ↑ Sedgewick, Robert (2002), Algorithms in C++: Graph Algorithms (3rd ed.), Pearson Education, pp. 149–157, ISBN 978-0-201-36118-6, https://books.google.com/books?id=0rLN_tcvD-IC&pg=PT149.
- ↑ 3.0 3.1 3.2 Soukup, Lajos (2008), "Infinite combinatorics: from finite to infinite", Horizons of Combinatorics, Bolyai Soc. Math. Stud., 17, Berlin: Springer, pp. 189–213, doi:10.1007/978-3-540-77200-2_10, ISBN 978-3-540-77199-9. See in particular Theorem 3, p. 193.
- ↑ 4.0 4.1 4.2 Diestel, Reinhard (2017), Graph Theory, Graduate Texts in Mathematics, 173 (5th ed.), Berlin: Springer, pp. 34–36, 220–221, 247, 251–252, doi:10.1007/978-3-662-53622-3, ISBN 978-3-662-53621-6, https://diestel-graph-theory.com/
- ↑ "Depth-first search is inherently sequential", Information Processing Letters 20 (5): 229–234, 1985, doi:10.1016/0020-0190(85)90024-9.
- ↑ 6.0 6.1 Aggarwal, A.; Anderson, R. J. (1988), "A random NC algorithm for depth first search", Combinatorica 8 (1): 1–12, doi:10.1007/BF02122548.
- ↑ "An NC algorithm for minimum cuts", SIAM Journal on Computing 26 (1): 255–272, 1997, doi:10.1137/S0097539794273083.
- ↑ "On the expression of graph properties in some fragments of monadic second-order logic", Proc. Descr. Complex. Finite Models, DIMACS, 31, Amer. Math. Soc., 1996, pp. 33–62, http://www.labri.fr/perso/courcell/Textes/DIMACS(1997).pdf.
- ↑ "Randomly traceable graphs", SIAM Journal on Applied Mathematics 16 (4): 696–700, 1968, doi:10.1137/0116056.
- ↑ "Chapter 6. Bounded height trees and tree-depth", Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics, 28, Heidelberg: Springer, 2012, pp. 115–144, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7.
- ↑ de Fraysseix, Hubert (1982), "A depth-first-search characterization of planarity", Graph theory (Cambridge, 1981), Ann. Discrete Math., 13, Amsterdam: North-Holland, pp. 75–80; de Fraysseix, Hubert (2006), "Trémaux trees and planarity", International Journal of Foundations of Computer Science 17 (5): 1017–1029, doi:10.1142/S0129054106004248.
- ↑ Diestel, Reinhard (2001), "Normal spanning trees, Aronszajn trees and excluded minors", Journal of the London Mathematical Society, Second Series 63 (1): 16–32, doi:10.1112/S0024610700001708, http://www.math.uni-hamburg.de/research/papers/hbm/hbm2000105.pdf.
- ↑ Bowler, Nathan; Geschke, Stefan; Pitz, Max (2016), Minimal obstructions for normal spanning trees, Bibcode: 2016arXiv160901042B
- ↑ 14.0 14.1 Diestel, Reinhard (2006), "End spaces and spanning trees", Journal of Combinatorial Theory, Series B 96 (6): 846–854, doi:10.1016/j.jctb.2006.02.010.
 |