Ulam–Warburton automaton
The Ulam–Warburton cellular automaton (UWCA) is a 2-dimensional fractal pattern that grows on a regular grid of cells consisting of squares. Starting with one square initially ON and all others OFF, successive iterations are generated by turning ON all squares that share precisely one edge with an ON square. This is the von Neumann neighborhood. The automaton is named after the Polish-American mathematician and scientist Stanislaw Ulam[1] and the Scottish engineer, inventor and amateur mathematician Mike Warburton.[2][3]

Properties and relations
The UWCA is a 2D 5-neighbor outer totalistic cellular automaton using rule 686.[4]
The number of cells turned ON in each iteration is denoted with an explicit formula:
and for
where is the Hamming weight function which counts the number of 1's in the binary expansion of [5]
The minimum upper bound of summation for is such that
The total number of cells turned ON is denoted
Table of wt(n), u(n) and U(n)
The table shows that different inputs to can lead to the same output.
This surjective property emerges from the simple rule of growth – a new cell is born if it shares only one-edge with an existing ON cell - the process appears disorderly and is modeled by functions involving but within the chaos there is regularity.
| 0 | 0 | 0 | 0 | 10 | 2 | 12 | 101 |
| 1 | 1 | 1 | 1 | 11 | 3 | 12 | 113 |
| 2 | 1 | 4 | 5 | 12 | 2 | 36 | 149 |
| 3 | 2 | 4 | 9 | 13 | 3 | 12 | 161 |
| 4 | 1 | 12 | 21 | 14 | 3 | 36 | 197 |
| 5 | 2 | 4 | 25 | 15 | 4 | 36 | 233 |
| 6 | 2 | 12 | 37 | 16 | 1 | 108 | 341 |
| 7 | 3 | 12 | 49 | 17 | 2 | 4 | 345 |
| 8 | 1 | 36 | 85 | 18 | 2 | 12 | 357 |
| 9 | 2 | 4 | 89 | 19 | 3 | 12 | 369 |
is OEIS sequence A147562 and is OEIS sequence A147582
Counting cells with quadratics
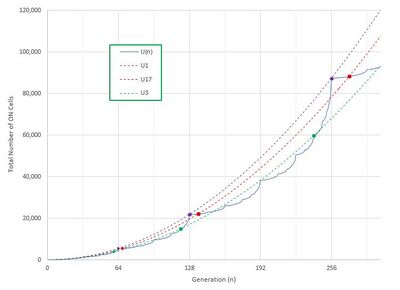
For all integer sequences of the form where and
Let
( is OEIS sequence A130665)
Then the total number of ON cells in the integer sequence is given by[6]
Or in terms of we have
Table of integer sequences nm and Um
| 0 | 1 | 1 | 3 | 9 | 5 | 25 | 7 | 49 |
| 1 | 2 | 5 | 6 | 37 | 10 | 101 | 14 | 197 |
| 2 | 4 | 21 | 12 | 149 | 20 | 405 | 28 | 789 |
| 3 | 8 | 85 | 24 | 597 | 40 | 1,621 | 56 | 3,157 |
| 4 | 16 | 341 | 48 | 2,389 | 80 | 6,485 | 112 | 12,629 |
| 5 | 32 | 1,365 | 96 | 9,557 | 160 | 25,941 | 224 | 50,517 |
Upper and lower bounds

has fractal-like behavior with a sharp upper bound for given by
The upper bound only contacts at 'high-water' points when .
These are also the generations at which the UWCA based on squares, the Hex–UWCA based on hexagons and the Sierpinski triangle return to their base shape.[7]

Limit superior and limit inferior
We have
The lower limit was obtained by Robert Price (OEIS sequence A261313 ) and took several weeks to compute and is believed to be twice the lower limit of where is the total number of toothpicks in the toothpick sequence up to generation [8]
Relationship to

Hexagonal UWCA
The Hexagonal-Ulam–Warburton cellular automaton (Hex-UWCA) is a 2-dimensional fractal pattern that grows on a regular grid of cells consisting of hexagons. The same growth rule for the UWCA applies and the pattern returns to a hexagon in generations , when the first hexagon is considered as generation . The UWCA has two reflection lines that pass through the corners of the initial cell dividing the square into four quadrants, similarly the Hex-UWCA has three reflection lines dividing the hexagon into six sections and the growth rule follows the symmetries. Cells whose centers lie on a line of reflection symmetry are never born.
The Hex-UWCA pattern can be explored here.
Sierpinski triangle

The Sierpinski triangle appears in 13th century Italian floor mosaics. Wacław Sierpiński described the triangle in 1915.
If we consider the growth of the triangle, with each row corresponding to a generation and the top row generation is a single triangle, then like the UWCA and the Hex-UWCA it returns to its starting shape, in generations
Toothpick sequence

The toothpick pattern is constructed by placing a single toothpick of unit length on a square grid, aligned with the vertical axis. At each subsequent stage, for every exposed toothpick end, place a perpendicular toothpick centred at that end. The resulting structure has a fractal-like appearance.
The toothpick and UWCA structures are examples of cellular automata defined on a graph and when considered as a subgraph of the infinite square grid the structure is a tree.
The toothpick sequence returns to its base rotated ‘H’ shape in generations where
The toothpick sequence and various toothpick-like sequences can be explored here.
Combinatorial game theory
A subtraction game called LIM, in which two players alternately modify three piles of tokens by taking an equal amount of tokens from two of the piles and adding the same amount to the third pile, has a set of winning positions that can be described using the Ulam–Warburton automaton.[9][10]
History
The beginnings of automata go back to a conversation Ulam had with Stanislaw Mazur in a coffee house in Lwów Poland when Ulam was twenty in 1929.[11] Ulam worked with John von Neumann during the war years when they became good friends and discussed cellular automaton. Von Neumann’s used these ideas in his concept of a universal constructor and the digital computer. Ulam focussed on biological and ‘crystal like’ patterns publishing a sketch of the growth of a square based cell structure using a simple rule in 1962. Mike Warburton is an amateur mathematician working in probabilistic number theory who was educated at George Heriot's School in Edinburgh. His son's mathematics GCSE coursework involved investigating the growth of equilateral triangles or squares in the Euclidean plane with the rule – a new generation is born if and only if connected to the last by only one-edge. That coursework concluded with a recursive formula for the number of ON cells born in each generation. Later, Warburton found the sharp upper bound formula which he wrote up as a note in the Open University’s M500 magazine in 2002. David Singmaster read the article, analysed the structure and named the object the Ulam-Warburton cellular automaton in his 2003 article. Since then it has given rise to numerous integer sequences.
References
- ↑ S. M. Ulam, On some mathematical problems connected with patterns of growth of figures, Mathematical Problems in BiologicalSciences, 14 (1962), 215–224.
- ↑ M. Warburton, One-edge connections, M500 Magazine of The Open University, 188 (2002), 11
- ↑ D. Singmaster, On the cellular automaton of Ulam and Warburton, M500 Magazine of The Open University, 195 (2003), 2–7
- ↑ OEIS - Index to 2D 5-Neighbor Cellular Automata,[1],
- ↑ Applegate, David; Pol, Omar E.; Sloane, N. J. A. (2010). "The Toothpick Sequence and Other Sequences from Cellular Automata". Congressus Numerant 206: 157–191.
- ↑ Mike Warburton, "Ulam-Warburton Automaton - Counting Cells with Quadratics ", arXiv:1901.10565
- ↑ Tanya Khovanova, Eric Nie, Alok Puranik, "The Sierpinski Triangle and the Ulam-Warburton Automaton", arXiv:1408.5937
- ↑ Steven R. Finch, Mathematical Constants II, 364-365
- ↑ Fink, Alex (May 2013), "LIM is not slim", International Journal of Game Theory 43 (2): 269–281, doi:10.1007/s00182-013-0380-z
- ↑ "Nim fractals", Journal of Integer Sequences 17 (7): Article 14.7.8, 17, 2014
- ↑ S. M. Ulam, Adventures of a Mathematician, p32
External links
- Explore the UWCA, Hex-UWCA and related integer sequence animations
- Neil Sloane: Terrific Toothpick Patterns - Numberphile. (The UWCA starts at time 8:20)
 |
