Visual angle

Diagram showing visual angle V.

If an object is close to the eye, the visual angle is relatively large, therefore the object is projected large on the retina. If the same object is further away, the area on the retina onto which it is projected is reduced.

Visual angle is the angle a viewed object subtends at the eye, usually stated in degrees of arc. It also is called the object's angular size.

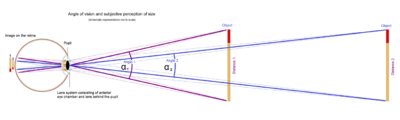
The diagram on the right shows an observer's eye looking at a frontal extent (the vertical arrow) that has a linear size [math]\displaystyle{ S }[/math], located in the distance [math]\displaystyle{ D }[/math] from point [math]\displaystyle{ O }[/math].

For present purposes, point [math]\displaystyle{ O }[/math] can represent the eye's nodal points at about the center of the lens, and also represent the center of the eye's entrance pupil that is only a few millimeters in front of the lens.

The three lines from object endpoint [math]\displaystyle{ A }[/math] heading toward the eye indicate the bundle of light rays that pass through the cornea, pupil and lens to form an optical image of endpoint [math]\displaystyle{ A }[/math] on the retina at point [math]\displaystyle{ a }[/math]. The central line of the bundle represents the chief ray.

The same holds for object point [math]\displaystyle{ B }[/math] and its retinal image at [math]\displaystyle{ b }[/math].

The visual angle [math]\displaystyle{ V }[/math] is the angle between the chief rays of [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math].

Measuring and computing

The visual angle [math]\displaystyle{ V }[/math] can be measured directly using a theodolite placed at point [math]\displaystyle{ O }[/math].

Or, it can be calculated (in radians) using the formula, [math]\displaystyle{ V = 2 \arctan\left(\frac{S}{2D}\right) }[/math].

However, for visual angles smaller than about 10 degrees, this simpler formula provides very close approximations:

[math]\displaystyle{ \tan\left( V \right) = \frac{S}{D}. }[/math]

The retinal image and visual angle

As the above sketch shows, a real image of the object is formed on the retina between points [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math]. (See visual system). For small angles, the size of this retinal image [math]\displaystyle{ R }[/math] is

[math]\displaystyle{ \frac{R}{n} = \tan V, }[/math]

where [math]\displaystyle{ n }[/math] is the distance from the nodal points to the retina, about 17 mm.

Examples

If one looks at a one-centimeter object at a distance of one meter and a two-centimeter object at a distance of two meters, both subtend the same visual angle of about 0.01 rad or 0.57°. Thus they have the same retinal image size [math]\displaystyle{ R \approx 0.17 \text{ mm} }[/math].

That is just a bit larger than the retinal image size for the moon, which is about [math]\displaystyle{ 0.15 \text{ mm} }[/math], because, with moon's mean diameter [math]\displaystyle{ S = 3474\text{ kilometers} }[/math] [math]\displaystyle{ (2159 \text{ miles}) }[/math] , and earth to moon mean distance [math]\displaystyle{ D }[/math] averaging [math]\displaystyle{ 383,000 \text{ kilometers} }[/math] ([math]\displaystyle{ 238,000 \text{ miles} }[/math]), [math]\displaystyle{ V \approx 0.009 \text{ rad} }[/math][math]\displaystyle{ \approx 0.52 \text{ deg} }[/math].

Also, for some easy observations, if one holds one's index finger at arm's length, the width of the index fingernail subtends approximately one degree, and the width of the thumb at the first joint subtends approximately two degrees.

Therefore, if one is interested in the performance of the eye or the first processing steps in the visual cortex, it does not make sense to refer to the absolute size of a viewed object (its linear size [math]\displaystyle{ S }[/math]). What matters is the visual angle [math]\displaystyle{ V }[/math] which determines the size of the retinal image.

Terminological confusions

In astronomy the term apparent size refers to the physical angle [math]\displaystyle{ V }[/math] or angular diameter.

But in psychophysics and experimental psychology the adjective "apparent" refers to a person's subjective experience. So, "apparent size" has referred to how large an object looks, also often called its "perceived size".

Additional confusion has occurred because there are two qualitatively different "size" experiences for a viewed object. One is the perceived visual angle [math]\displaystyle{ V' }[/math] (or apparent visual angle) which is the subjective correlate of [math]\displaystyle{ V }[/math], also called the object's perceived or apparent angular size. The perceived visual angle is best defined as the difference between the perceived directions of the object's endpoints from oneself.

The other "size" experience is the object's perceived linear size [math]\displaystyle{ S' }[/math] (or apparent linear size) which is the subjective correlate of [math]\displaystyle{ S }[/math], the object's physical width or height or diameter.

Widespread use of the ambiguous terms "apparent size" and "perceived size" without specifying the units of measure has caused confusion.

Representation of visual angle in visual cortex

The brain's primary visual cortex (area V1 or Brodmann area 17) contains a spatially isomorphic representation of the retina (see retinotopy). Loosely speaking, it is a distorted "map" of the retina. Accordingly, the size [math]\displaystyle{ R }[/math] of a given retinal image determines the extent of the neural activity pattern eventually generated in area V1 by the associated retinal activity pattern. Murray, Boyaci, & Kersten (2006) recently used Functional magnetic resonance imaging (fMRI) to show that an increase in a viewed target's visual angle, which increases [math]\displaystyle{ R }[/math], also increases the extent of the corresponding neural activity pattern in area V1.

The observers in experiment carried out by Murray and colleagues viewed a flat picture with two discs that subtended the same visual angle [math]\displaystyle{ V }[/math] and formed retinal images of the same size [math]\displaystyle{ R }[/math], but the perceived angular size [math]\displaystyle{ V' }[/math] of one was about 17% larger than for the other, due to differences in the background patterns for the disks. It was shown that the areas of the activity in V1 related to the disks were of unequal size, despite the fact that the retinal images were the same size. This size difference in area V1 correlated with the 17% illusory difference between the perceived visual angles. This finding has implications for spatial illusions such as the visual angle illusion.

See also

• Visual acuity
• Visual angle illusion

References

• Baird, J. C. (1970). Psychophysical analysis of visual space. Oxford, London: Pergamon Press.
• Joynson, R. B. (1949). The problem of size and distance. Quarterly Journal of Experimental Psychology, 1, 119–135.
• McCready, D. (1965). Size-distance perception and accommodation-convergence micropsia: A critique. Vision Research. 5, 189–206.
• McCready, D. (1985). On size, distance and visual angle perception. Perception & Psychophysics, 37, 323–334.
• Murray, S.O., Boyaci, H, & Kersten, D. (2006) The representation of perceived angular size in human primary visual cortex. Nature Neuroscience, 9, 429–434 (1 March 2006).
• McCready, D. The Moon Illusion Explained.

External links

• The University at Buffalo's Interactive Visual Acuity Chart for the display of letters or symbols for a specified Snellen line on your computer monitor at exactly the right size (note: you must follow the instructions for calibration).