Astronomy:Angular diameter

Short description: How large a sphere or circle appears

The angular diameter, angular size, apparent diameter, or apparent size is an angular distance describing how large a sphere or circle appears from a given point of view. In the vision sciences, it is called the visual angle, and in optics, it is the angular aperture (of a lens). The angular diameter can alternatively be thought of as the angular displacement through which an eye or camera must rotate to look from one side of an apparent circle to the opposite side. Humans can resolve with their naked eyes diameters of up to about 1 arcminute (approximately 0.017° or 0.0003 radians). This corresponds to 0.3 m at a 1 km distance, or to perceiving Venus as a disk under optimal conditions.

Formula

Diagram for the formula of the angular diameter

The angular diameter of a circle whose plane is perpendicular to the displacement vector between the point of view and the center of said circle can be calculated using the formula

[math]\displaystyle{ \delta = 2\arctan \left(\frac{d}{2D}\right), }[/math]

in which [math]\displaystyle{ \delta }[/math] is the angular diameter in degrees, and [math]\displaystyle{ d }[/math] is the actual diameter of the object, and [math]\displaystyle{ D }[/math] is the distance to the object. When [math]\displaystyle{ D \gg d }[/math], we have [math]\displaystyle{ \delta \approx d / D }[/math], and the result obtained is in radians.

For a spherical object whose actual diameter equals [math]\displaystyle{ d_\mathrm{act}, }[/math] and where [math]\displaystyle{ D }[/math] is the distance to the center of the sphere, the angular diameter can be found by the formula

[math]\displaystyle{ \delta = 2\arcsin \left(\frac{d_\mathrm{act}}{2D}\right) }[/math]

The difference is due to the fact that the apparent edges of a sphere are its tangent points, which are closer to the observer than the center of the sphere. The difference is significant only for spherical objects of large angular diameter, since the following small-angle approximations hold for small values of [math]\displaystyle{ x }[/math]:

[math]\displaystyle{ \arcsin x \approx \arctan x \approx x. }[/math]

Estimating angular diameter using the hand

Approximate angles of 10°, 20°, 5°, and 1° for the hand outstretched arm's length

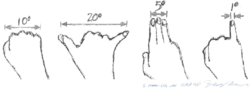
Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.

Use in astronomy

Angular diameter: the angle subtended by an object

In astronomy, the sizes of celestial objects are often given in terms of their angular diameter as seen from Earth, rather than their actual sizes. Since these angular diameters are typically small, it is common to present them in arcseconds (″). An arcsecond is 1/3600th of one degree (1°) and a radian is 180/π degrees. So one radian equals 3,600 × 180/[math]\displaystyle{ \pi }[/math] arcseconds, which is about 206,265 arcseconds (1 rad ≈ 206,264.806247"). Therefore, the angular diameter of an object with physical diameter d at a distance D, expressed in arcseconds, is given by:

[math]\displaystyle{ \delta = 206,265 ~ (d / D) ~ \mathrm{arcseconds} }[/math].

These objects have an angular diameter of 1″:

• an object of diameter 1 cm at a distance of 2.06 km
• an object of diameter 725.27 km at a distance of 1 astronomical unit (AU)
• an object of diameter 45 866 916 km at 1 light-year
• an object of diameter 1 AU (149 597 871 km) at a distance of 1 parsec (pc)

Thus, the angular diameter of Earth's orbit around the Sun as viewed from a distance of 1 pc is 2″, as 1 AU is the mean radius of Earth's orbit.

The angular diameter of the Sun, from a distance of one light-year, is 0.03″, and that of Earth 0.0003″. The angular diameter 0.03″ of the Sun given above is approximately the same as that of a human body at a distance of the diameter of Earth.

This table shows the angular sizes of noteworthy celestial bodies as seen from Earth:

Celestial object	Angular diameter or size	Relative size
Magellanic Stream	over 100°
Gum Nebula	36°
Milky Way	30° (by 360°)
Width of spread out hand with arm streched out	20°	353 meter at 1 km distance
Serpens-Aquila Rift	20° by 10°
Canis Major Overdensity	12° by 12°
Smith's Cloud	11°
Large Magellanic Cloud	10.75° by 9.17°	Note: brightest galaxy, other than the Milky Way, in the night sky (0.9 apparent magnitude (V))
Barnard's loop	10°
Zeta Ophiuchi Sh2-27 nebula	10°
Width of fist with arm streched out	10°	175 meter at 1 km distance
Sagittarius Dwarf Spheroidal Galaxy	7.5° by 3.6°
Northern Coalsack Nebula	7° by 5°
Coalsack nebula	7° by 5°
Cygnus OB7	4° by 7°
Rho Ophiuchi cloud complex	4.5° by 6.5°
Hyades	5°30′	Note: brightest star cluster in the night sky, 0.5 apparent magnitude (V)
Small Magellanic Cloud	5°20′ by 3°5′
Andromeda Galaxy	3°10′ by 1°	About six times the size of the Sun or the Moon. Only the much smaller core is visible without long-exposure photography.
Charon (from the surface of Pluto)	3°9’
Veil Nebula	3°
Heart Nebula	2.5° by 2.5°
Westerhout 5	2.3° by 1.25°
Sh2-54	2.3°
Carina Nebula	2° by 2°	Note: brightest nebula in the night sky, 1.0 apparent magnitude (V)
North America Nebula	2° by 100′
Earth in the Moon's sky	2° - 1°48′	Appearing about three to four times larger than the Moon in Earth's sky
Orion Nebula	1°5′ by 1°
Width of little finger with arm streched out	1°	17.5 meter at 1 km distance
Io (as seen from the “surface” of Jupiter)	35’ 35”
Moon	34′6″ – 29′20″	32.5–28 times the maximum value for Venus (orange bar below) / 2046–1760″ the Moon has a diameter of 3,474 km
Sun	32′32″ – 31′27″	31–30 times the maximum value for Venus (orange bar below) / 1952–1887″ the Sun has a diameter of 1,391,400 km
Triton (From the “surface” of Neptune)	28’ 11”
Angular size of the distance between Earth and the Moon as viewed from Mars, at inferior conjunction	about 25′
Ariel (From the “surface” of Uranus)	24’ 11”
Ganymede (From the “surface” of Jupiter)	18’ 6”
Europa (From the “surface” of Jupiter)	17’ 51”
Umbriel ( (From the “surface” of Uranus)	16’ 42”
Helix Nebula	about 16′ by 28′
Spire in Eagle Nebula	4′40″	length is 280″
Venus	1′6″ – 0′9.7″
International Space Station (ISS)	1′3″	the ISS has a width of about 108 m
Minimum resolvable diameter by the human eye	1′	0.3 meter at 1 km distance
About 100 km on the surface of the Moon	1′	Comparable to the size of features like large lunar craters, such as the Copernicus crater, a prominent bright spot in the eastern part of Oceanus Procellarum on the waning side, or the Tycho crater within a bright area in the south, of the lunar near side.
Jupiter	50.1″ – 29.8″
Minimum resolvable gap between two lines by the human eye	40″	a gap of 0.026 mm as viewed from 15 cm away
Mars	25.1″ – 3.5″
Apparent size of Sun, seen from 90377 Sedna at aphelion	20.4"
Saturn	20.1″ – 14.5″
Mercury	13.0″ – 4.5″
Uranus	4.1″ – 3.3″
Neptune	2.4″ – 2.2″
Ganymede	1.8″ – 1.2″	Ganymede has a diameter of 5,268 km
An astronaut (~1.7 m) at a distance of 350 km, the average altitude of the ISS	1″
Minimum resolvable diameter by Galileo Galilei's largest 38mm refracting telescopes	~1″	Note: 30x magnification, comparable to very strong contemporary terrestrial binoculars
Ceres	0.84″ – 0.33″
Vesta	0.64″ – 0.20″
Pluto	0.11″ – 0.06″
Eris	0.089″ – 0.034″
R Doradus	0.062″ – 0.052″	Note: R Doradus is thought to be the extrasolar star with the largest apparent size as viewed from Earth
Betelgeuse	0.060″ – 0.049″
Alphard	0.00909″
Rho Cassiopeiae	0.0072″
Alpha Centauri A	0.007″
Canopus	0.006″
Sirius	0.005936″
Altair	0.003″
Deneb	0.002″
Proxima Centauri	0.001″
Alnitak	0.0005″
Proxima Centauri b	0.00008″
Event horizon of black hole M87* at center of the M87 galaxy, imaged by the Event Horizon Telescope in 2019.	0.000025″ (2.5×10−5)	Comparable to a tennis ball on the Moon
A star like Alnitak at a distance where the Hubble Space Telescope would just be able to see it	6×10−10 arcsec

Log-log plot of aperture diameter vs angular resolution at the diffraction limit for various light wavelengths compared with various astronomical instruments. For example, the blue star shows that the Hubble Space Telescope is almost diffraction-limited in the visible spectrum at 0.1 arcsecs, whereas the red circle shows that the human eye should have a resolving power of 20 arcsecs in theory, though normally only 60 arcsecs.

Comparison of angular diameter of the Sun, Moon and planets. To get a true representation of the sizes, view the image at a distance of 103 times the width of the "Moon: max." circle. For example, if this circle is 5 cm wide on your monitor, view it from 5.15 m away.

This photo compares the apparent sizes of Jupiter and its four Galilean moons (Callisto at maximum elongation) with the apparent diameter of the full Moon during their conjunction on 10 April 2017.

The angular diameter of the Sun, as seen from Earth, is about 250,000 times that of Sirius. (Sirius has twice the diameter and its distance is 500,000 times as much; the Sun is 10¹⁰ times as bright, corresponding to an angular diameter ratio of 10⁵, so Sirius is roughly 6 times as bright per unit solid angle.)

The angular diameter of the Sun is also about 250,000 times that of Alpha Centauri A (it has about the same diameter and the distance is 250,000 times as much; the Sun is 4×10¹⁰ times as bright, corresponding to an angular diameter ratio of 200,000, so Alpha Centauri A is a little brighter per unit solid angle).

The angular diameter of the Sun is about the same as that of the Moon. (The Sun's diameter is 400 times as large and its distance also; the Sun is 200,000 to 500,000 times as bright as the full Moon (figures vary), corresponding to an angular diameter ratio of 450 to 700, so a celestial body with a diameter of 2.5–4″ and the same brightness per unit solid angle would have the same brightness as the full Moon.)

Even though Pluto is physically larger than Ceres, when viewed from Earth (e.g., through the Hubble Space Telescope) Ceres has a much larger apparent size.

Angular sizes measured in degrees are useful for larger patches of sky. (For example, the three stars of the Belt cover about 4.5° of angular size.) However, much finer units are needed to measure the angular sizes of galaxies, nebulae, or other objects of the night sky.

Degrees, therefore, are subdivided as follows:

• 360 degrees (°) in a full circle
• 60 arc-minutes (′) in one degree
• 60 arc-seconds (″) in one arc-minute

To put this in perspective, the full Moon as viewed from Earth is about ​¹⁄₂°, or 30′ (or 1800″). The Moon's motion across the sky can be measured in angular size: approximately 15° every hour, or 15″ per second. A one-mile-long line painted on the face of the Moon would appear from Earth to be about 1″ in length.

Minimum, mean and maximum distances of the Moon from Earth with its angular diameter as seen from Earth's surface, to scale

In astronomy, it is typically difficult to directly measure the distance to an object, yet the object may have a known physical size (perhaps it is similar to a closer object with known distance) and a measurable angular diameter. In that case, the angular diameter formula can be inverted to yield the angular diameter distance to distant objects as

[math]\displaystyle{ d \equiv 2 D \tan \left( \frac{\delta}{2} \right). }[/math]

In non-Euclidean space, such as our expanding universe, the angular diameter distance is only one of several definitions of distance, so that there can be different "distances" to the same object. See Distance measures (cosmology).

Non-circular objects

Many deep-sky objects such as galaxies and nebulae appear non-circular and are thus typically given two measures of diameter: major axis and minor axis. For example, the Small Magellanic Cloud has a visual apparent diameter of 5° 20′ × 3° 5′.

Defect of illumination

Defect of illumination is the maximum angular width of the unilluminated part of a celestial body seen by a given observer. For example, if an object is 40″ of arc across and is 75% illuminated, the defect of illumination is 10″.

See also

• Angular diameter distance
• Angular resolution
• Solid angle
• Visual acuity
• Visual angle
• Perceived visual angle
• List of stars with resolved images
• Apparent magnitude

External links

• Small-Angle Formula (archived 7 October 1997)
• Visual Aid to the Apparent Size of the Planets