Wave surface

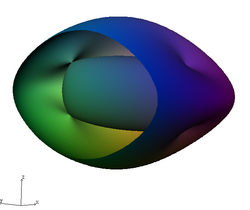
In mathematics, Fresnel's wave surface, found by Augustin-Jean Fresnel in 1822, is a quartic surface describing the propagation of light in an optically biaxial crystal. Wave surfaces are special cases of tetrahedroids which are in turn special cases of Kummer surfaces.

In projective coordinates (w:x:y:z) the wave surface is given by

[math]\displaystyle{ \frac{a^2x^2}{x^2+y^2+z^2-a^2w^2} + \frac{b^2y^2}{x^2+y^2+z^2-b^2w^2} + \frac{c^2z^2}{x^2+y^2+z^2-c^2w^2} =0 }[/math]

Fresnel's Wave Surface, a quartic surface describing the propagation of light in an optically biaxial crystal, [math]\displaystyle{ a=1, b=0.5, c=1.5, w=1 }[/math].

References

• Bateman, H. (1910), "Kummer's quartic surface as a wave surface.", Proceedings of the London Mathematical Society 8 (1): 375–382, doi:10.1112/plms/s2-8.1.375, ISSN 0024-6115, https://zenodo.org/record/1447806 
• Cayley, Arthur (1846), "Sur la surface des ondes", Journal de Mathématiques Pures et Appliquées 11: 291–296, Collected papers vol 1 pages 302–305 
• Fresnel, A. (1822), "Second supplément au mémoire sur la double réfraction" (signed 31 March 1822, submitted 1 April 1822),  in  H. de Sénarmont, É. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel, Paris: Imprimerie Impériale (3 vols., 1866–70), vol. 2 (1868), pp. 369–442, especially pp. 369 (date présenté), 386–8 (eq. 4), 442 (signature and date).
• Knörrer, H. (1986), "Die Fresnelsche Wellenfläche", Arithmetik und Geometrie, Math. Miniaturen, 3, Basel, Boston, Berlin: Birkhäuser, pp. 115–141, ISBN 978-3-7643-1759-1, https://archive.org/details/arithmetikundgeo0000unse/page/115 
• Love, A. E. H. (2011), A treatise on the Mathematical Theory of Elasticity, Dover Publications, New York, ISBN 978-0-486-60174-8, https://books.google.com/books?id=ViebCriF-ssC 

External links

• Fresnel wave surface