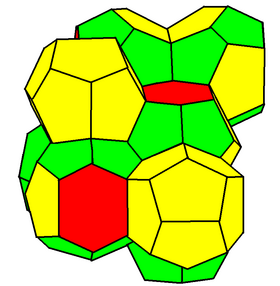
Weaire–Phelan structure

From HandWiki
Weaire–Phelan structure
Weaire–Phelan structure (polyhedral cells)
Space group
Fibrifold notation
Coxeter notation		 Pm3n (223)
2o
[[4,3,4]+]

In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure.[1]

History and the Kelvin problem

The bitruncated cubic honeycomb, a convex honeycomb whose truncated octahedron cells are deformed slightly to form the Kelvin structure

In two dimensions, the subdivision of the plane into cells of equal area with minimum average perimeter is given by the hexagonal tiling, but although the first record of this honeycomb conjecture goes back to the ancient Roman scholar Marcus Terentius Varro, it was not proven until the work of Thomas C. Hales in 1999.[2] In 1887, Lord Kelvin asked the corresponding question for three-dimensional space: how can space be partitioned into cells of equal volume with the least area of surface between them? Or, in short, what was the most efficient soap bubble foam?[3] This problem has since been referred to as the Kelvin problem.

Kelvin proposed a foam called the Kelvin structure. His foam is based on the bitruncated cubic honeycomb, a convex uniform honeycomb formed by the truncated octahedron, a space-filling convex polyhedron with 6 square faces and 8 hexagonal faces. However, this honeycomb does not satisfy Plateau's laws, formulated by Joseph Plateau in the 19th century, according to which minimal foam surfaces meet at [math]\displaystyle{ 120^\circ }[/math] angles at their edges, with these edges meeting each other in sets of four with angles of [math]\displaystyle{ \arccos\tfrac{1}{3}\approx 109.47^\circ }[/math]. The angles of the polyhedral structure are different; for instance, its edges meet at angles of [math]\displaystyle{ 90^\circ }[/math] on square faces, or [math]\displaystyle{ 120^\circ }[/math] on hexagonal faces. Therefore, Kelvin's proposed structure uses curvilinear edges and slightly warped minimal surfaces for its faces, obeying Plateau's laws and reducing the area of the structure by 0.2% compared with the corresponding polyhedral structure.[1][3]

Although Kelvin did not state it explicitly as a conjecture,[4] the idea that the foam of the bitruncated cubic honeycomb is the most efficient foam, and solves Kelvin's problem, became known as the Kelvin conjecture. It was widely believed, and no counter-example was known for more than 100 years. Finally, in 1993, Trinity College Dublin physicist Denis Weaire and his student Robert Phelan discovered the Weaire–Phelan structure through computer simulations of foam, and showed that it was more efficient, disproving the Kelvin conjecture.[1]

Since the discovery of the Weaire–Phelan structure, other counterexamples to the Kelvin conjecture have been found, but the Weaire–Phelan structure continues to have the smallest known surface area per cell of these counterexamples.[5][6][7] Although numerical experiments suggest that the Weaire–Phelan structure is optimal, this remains unproven.[8] In general, it has been very difficult to prove the optimality of structures involving minimal surfaces. The minimality of the sphere as a surface enclosing a single volume was not proven until the 19th century, and the next simplest such problem, the double bubble conjecture on enclosing two volumes, remained open for over 100 years until being proven in 2002.[9]

Description

Irregular dodecahedron
Tetrakaidecahedron

The Weaire–Phelan structure differs from Kelvin's in that it uses two kinds of cells, although they have equal volume. Like the cells in Kelvin's structure, these cells are combinatorially equivalent to convex polyhedra. One is a pyritohedron, an irregular dodecahedron with pentagonal faces, possessing tetrahedral symmetry (Th). The second is a form of truncated hexagonal trapezohedron, a species of tetrakaidecahedron with two hexagonal and twelve pentagonal faces, in this case only possessing two mirror planes and a rotoreflection symmetry. Like the hexagons in the Kelvin structure, the pentagons in both types of cells are slightly curved. The surface area of the Weaire–Phelan structure is 0.3% less than that of the Kelvin structure.[1]

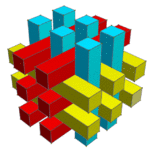
Tetrastix, modeling the face-to-face chains of tetrakaidecahedron cells in the Weaire–Phelan structure

The tetrakaidecahedron cells, linked up in face-to-face chains of cells along their hexagonal faces, form chains in three perpendicular directions. A combinatorially equivalent structure to the Weaire–Phelan structure can be made as a tiling of space by unit cubes, lined up face-to-face into infinite square prisms in the same way to form a structure of interlocking prisms called tetrastix. These prisms surround cubical voids which form one fourth of the cells of the cubical tiling; the remaining three fourths of the cells fill the prisms, offset by half a unit from the integer grid aligned with the prism walls. Similarly, in the Weaire–Phelan structure itself, which has the same symmetries as the tetrastix structure, 1/4 of the cells are dodecahedra and 3/4 are tetrakaidecahedra.[10]

The polyhedral honeycomb associated with the Weaire–Phelan structure (obtained by flattening the faces and straightening the edges) is also referred to loosely as the Weaire–Phelan structure. It was known well before the Weaire–Phelan structure was discovered, but the application to the Kelvin problem was overlooked.[11]

Applications

In physical systems

A close-up of the mold used for the growth of ordered liquid foams.

Experiments have shown that, with favorable boundary conditions, equal-volume bubbles spontaneously self-assemble into the Weaire–Phelan structure.[12][13]

The associated polyhedral honeycomb is found in two related geometries of crystal structure in chemistry. Where the components of the crystal lie at the centres of the polyhedra it forms one of the Frank–Kasper phases, the A15 phase.[14]

Where the components of the crystal lie at the corners of the polyhedra, it is known as the "Type I clathrate structure". Gas hydrates formed by methane, propane and carbon dioxide at low temperatures have a structure in which water molecules lie at the nodes of the Weaire–Phelan structure and are hydrogen bonded together, and the larger gas molecules are trapped in the polyhedral cages.[11] Some alkali metal hydrides silicides and germanides also form this structure, with silicon or germanium at nodes, and alkali metals in cages.[1][15][16]

In architecture

Beijing National Aquatics Centre

The Weaire–Phelan structure is the inspiration for the design by Tristram Carfrae of the Beijing National Aquatics Centre, the 'Water Cube', for the 2008 Summer Olympics.[17]

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 Weaire, D.; Phelan, R. (1994), "A counter-example to Kelvin's conjecture on minimal surfaces", Phil. Mag. Lett. 69 (2): 107–110, doi:10.1080/09500839408241577, Bibcode: 1994PMagL..69..107W .
  2. ↑ "The honeycomb conjecture", Discrete & Computational Geometry 25 (1): 1–22, 2001, doi:10.1007/s004540010071 
  3. ↑ 3.0 3.1 Lord Kelvin (Sir William Thomson) (1887), "On the Division of Space with Minimum Partitional Area", Philosophical Magazine 24 (151): 503, doi:10.1080/14786448708628135, http://soft-matter.seas.harvard.edu/images/1/17/Kelvin_Cell.pdf .
  4. ↑ (Weaire Phelan) write that it is "implicit rather than directly stated in Kelvin's original papers"
  5. ↑ Sullivan, John M. (1999), "The geometry of bubbles and foams", Foams and emulsions (Cargèse, 1997), NATO Advanced Science Institutes Series E: Applied Sciences, 354, Kluwer, pp. 379–402 
  6. ↑ Gabbrielli, Ruggero (1 August 2009), "A new counter-example to Kelvin's conjecture on minimal surfaces", Philosophical Magazine Letters 89 (8): 483–491, doi:10.1080/09500830903022651, ISSN 0950-0839, Bibcode: 2009PMagL..89..483G 
  7. ↑ Freiberger, Marianne (24 September 2009), "Kelvin's bubble burst again" (in en), Plus Magazine (University of Cambridge), https://plus.maths.org/content/kelvins-bubble-burst-again, retrieved 4 July 2017 
  8. ↑ Oudet, Édouard (2011), "Approximation of partitions of least perimeter by Γ-convergence: around Kelvin's conjecture", Experimental Mathematics 20 (3): 260–270, doi:10.1080/10586458.2011.565233, http://projecteuclid.org/euclid.em/1317924419 
  9. ↑ "Chapter 14. Proof of Double Bubble Conjecture", Geometric Measure Theory: A Beginner's Guide (4th ed.), Academic Press, 2009 .
  10. ↑ Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008), "Understanding the Irish Bubbles", The Symmetries of Things, Wellesley, Massachusetts: A K Peters, p. 351, ISBN 978-1-56881-220-5, https://books.google.com/books?id=Drj1CwAAQBAJ&pg=PA351 
  11. ↑ 11.0 11.1 Pauling (1960), The Nature of the Chemical Bond (3rd ed.), Cornell University Press, p. 471, https://archive.org/details/natureofchemical00paul 
  12. ↑ Gabbrielli, R.; Meagher, A.J.; Weaire, D.; Brakke, K.A.; Hutzler, S. (2012), "An experimental realization of the Weaire-Phelan structure in monodisperse liquid foam", Phil. Mag. Lett. 92 (1): 1–6, doi:10.1080/09500839.2011.645898, Bibcode: 2012PMagL..92....1G, http://www.tara.tcd.ie/bitstream/2262/67284/1/An%20experimental%20realisation%20of%20the%20Weaire-Phelan%20structure%20in%20%20monodisperse%20liquid%20foam.pdf .
  13. ↑ Ball, Philip (2011), "Scientists make the 'perfect' foam: Theoretical low-energy foam made for real", Nature, doi:10.1038/nature.2011.9504 .
  14. ↑ Frank, F. C.; Kasper, J. S. (1958), "Complex alloy structures regarded as sphere packings. I. Definitions and basic principles", Acta Crystallogr. 11 (3): 184–190, doi:10.1107/s0365110x58000487, http://journals.iucr.org/q/issues/1958/03/00/a02207/a02207.pdf . Frank, F. C.; Kasper, J. S. (1959), "Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures", Acta Crystallogr. 12 (7): 483–499, doi:10.1107/s0365110x59001499 .
  15. ↑ Kasper, J. S.; Hagenmuller, P.; Pouchard, M.; Cros, C. (December 1965), "Clathrate structure of silicon Na8Si46 and NaxSi136 (x < 11)", Science 150 (3704): 1713–1714, doi:10.1126/science.150.3704.1713, PMID 17768869, Bibcode: 1965Sci...150.1713K 
  16. ↑ Cros, Christian; Pouchard, Michel; Hagenmuller, Paul (December 1970), "Sur une nouvelle famille de clathrates minéraux isotypes des hydrates de gaz et de liquides, interprétation des résultats obtenus", Journal of Solid State Chemistry 2 (4): 570–581, doi:10.1016/0022-4596(70)90053-8, Bibcode: 1970JSSCh...2..570C 
  17. ↑ Fountain, Henry (August 5, 2008), "A Problem of Bubbles Frames an Olympic Design", New York Times, https://www.nytimes.com/2008/08/05/sports/olympics/05swim.html 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Weaire–Phelan_structure&oldid=3388369"