Weierstrass–Enneper parameterization

Short description: Construction for minimal surfaces

In mathematics, the Weierstrass–Enneper parameterization of minimal surfaces is a classical piece of differential geometry.

Alfred Enneper and Karl Weierstrass studied minimal surfaces as far back as 1863.

Weierstrass parameterization facilities fabrication of periodic minimal surfaces

Let [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] be functions on either the entire complex plane or the unit disk, where [math]\displaystyle{ g }[/math] is meromorphic and [math]\displaystyle{ f }[/math] is analytic, such that wherever [math]\displaystyle{ g }[/math] has a pole of order [math]\displaystyle{ m }[/math], [math]\displaystyle{ f }[/math] has a zero of order [math]\displaystyle{ 2m }[/math] (or equivalently, such that the product [math]\displaystyle{ f g^2 }[/math] is holomorphic), and let [math]\displaystyle{ c_1,c_2,c_3 }[/math] be constants. Then the surface with coordinates [math]\displaystyle{ (x_1, x_2, x_3) }[/math] is minimal, where the [math]\displaystyle{ x_k }[/math] are defined using the real part of a complex integral, as follows: [math]\displaystyle{ \begin{align} x_k(\zeta) &{}= \Re \left\{ \int_{0}^{\zeta} \varphi_{k}(z) \, dz \right\} + c_k , \qquad k=1,2,3 \\ \varphi_1 &{}= f(1-g^2)/2 \\ \varphi_2 &{}= \mathbf{i} f(1+g^2)/2 \\ \varphi_3 &{}= fg \end{align} }[/math]

The converse is also true: every nonplanar minimal surface defined over a simply connected domain can be given a parametrization of this type.

For example, Enneper's surface has f(z) = 1, g(z) = z^m.

Parametric surface of complex variables

The Weierstrass-Enneper model defines a minimal surface [math]\displaystyle{ X }[/math] ([math]\displaystyle{ \Reals^3 }[/math]) on a complex plane ([math]\displaystyle{ \Complex }[/math]). Let [math]\displaystyle{ \omega=u+v i }[/math] (the complex plane as the [math]\displaystyle{ uv }[/math] space), the Jacobian matrix of the surface can be written as a column of complex entries: [math]\displaystyle{ \mathbf{J} = \begin{bmatrix} \left( 1 - g^2(\omega) \right)f(\omega) \\ i\left( 1+ g^2(\omega) \right)f(\omega) \\ 2g(\omega) f(\omega) \end{bmatrix} }[/math] where [math]\displaystyle{ f(\omega) }[/math] and [math]\displaystyle{ g(\omega) }[/math] are holomorphic functions of [math]\displaystyle{ \omega }[/math].

The Jacobian [math]\displaystyle{ \mathbf{J} }[/math] represents the two orthogonal tangent vectors of the surface: [math]\displaystyle{ \mathbf{X_u} = \begin{bmatrix} \operatorname{Re}\mathbf{J}_1 \\ \operatorname{Re}\mathbf{J}_2 \\ \operatorname{Re} \mathbf{J}_3 \end{bmatrix} \;\;\;\; \mathbf{X_v} = \begin{bmatrix} -\operatorname{Im}\mathbf{J}_1 \\ -\operatorname{Im}\mathbf{J}_2 \\ -\operatorname{Im} \mathbf{J}_3 \end{bmatrix} }[/math]

The surface normal is given by [math]\displaystyle{ \mathbf{\hat{n}} = \frac{\mathbf{X_u}\times \mathbf{X_v}}{|\mathbf{X_u}\times \mathbf{X_v}|} = \frac{1}{| g|^2+1} \begin{bmatrix} 2\operatorname{Re} g \\ 2\operatorname{Im} g \\ | g|^2-1 \end{bmatrix} }[/math]

The Jacobian [math]\displaystyle{ \mathbf{J} }[/math] leads to a number of important properties: [math]\displaystyle{ \mathbf{X_u} \cdot \mathbf{X_v}=0 }[/math], [math]\displaystyle{ \mathbf{X_u}^2 = \operatorname{Re}(\mathbf{J}^2) }[/math], [math]\displaystyle{ \mathbf{X_v}^2 = \operatorname{Im}(\mathbf{J}^2) }[/math], [math]\displaystyle{ \mathbf{X_{uu}} + \mathbf{X_{vv}}=0 }[/math]. The proofs can be found in Sharma's essay: The Weierstrass representation always gives a minimal surface. The derivatives can be used to construct the first fundamental form matrix: [math]\displaystyle{ \begin{bmatrix} \mathbf{X_u} \cdot \mathbf{X_u} & \;\; \mathbf{X_u} \cdot \mathbf{X_v}\\ \mathbf{X_v} \cdot \mathbf{X_u} & \;\;\mathbf{X_v} \cdot \mathbf{X_v} \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} }[/math]

and the second fundamental form matrix [math]\displaystyle{ \begin{bmatrix} \mathbf{X_{uu}} \cdot \mathbf{\hat{n}} & \;\; \mathbf{X_{uv}} \cdot \mathbf{\hat{n}}\\ \mathbf{X_{vu}} \cdot \mathbf{\hat{n}} & \;\; \mathbf{X_{vv}} \cdot \mathbf{\hat{n}} \end{bmatrix} }[/math]

Finally, a point [math]\displaystyle{ \omega_t }[/math] on the complex plane maps to a point [math]\displaystyle{ \mathbf{X} }[/math] on the minimal surface in [math]\displaystyle{ \R^3 }[/math] by [math]\displaystyle{ \mathbf{X}= \begin{bmatrix} \operatorname{Re} \int_{\omega_0}^{\omega_ t}\mathbf{J}_1 d\omega\\ \operatorname{Re} \int_{\omega_0}^{\omega_ t} \mathbf{J}_2 d\omega\\ \operatorname{Re} \int_{\omega_0}^{\omega_ t} \mathbf{J}_3 d\omega \end{bmatrix} }[/math] where [math]\displaystyle{ \omega_0 = 0 }[/math] for all minimal surfaces throughout this paper except for Costa's minimal surface where [math]\displaystyle{ \omega_0=(1+i)/2 }[/math].

Embedded minimal surfaces and examples

The classical examples of embedded complete minimal surfaces in [math]\displaystyle{ \mathbb{R}^3 }[/math] with finite topology include the plane, the catenoid, the helicoid, and the Costa's minimal surface. Costa's surface involves Weierstrass's elliptic function [math]\displaystyle{ \wp }[/math]: [math]\displaystyle{ g(\omega)=\frac{A}{\wp' (\omega)} }[/math] [math]\displaystyle{ f(\omega)= \wp(\omega) }[/math] where [math]\displaystyle{ A }[/math] is a constant.

Helicatenoid

Choosing the functions [math]\displaystyle{ f(\omega) = e^{-i \alpha}e^{\omega/A} }[/math] and [math]\displaystyle{ g(\omega) = e^{-\omega/A} }[/math], a one parameter family of minimal surfaces is obtained.

[math]\displaystyle{ \varphi_1 = e^{-i \alpha} \sinh\left(\frac{\omega}{A}\right) }[/math] [math]\displaystyle{ \varphi_2 = i e^{-i \alpha} \cosh\left(\frac{\omega}{A}\right) }[/math] [math]\displaystyle{ \varphi_3 = e^{-i \alpha} }[/math] [math]\displaystyle{ \mathbf{X}(\omega) = \operatorname{Re} \begin{bmatrix} e^{-i\alpha} A \cosh \left( \frac{\omega}{A} \right) \\ i e^{-i\alpha} A \sinh \left( \frac{\omega}{A} \right) \\ e^{-i\alpha} \omega \\ \end{bmatrix} = \cos(\alpha) \begin{bmatrix} A \cosh \left( \frac{\operatorname{Re}(\omega)}{A} \right) \cos \left( \frac{\operatorname{Im}(\omega)}{A} \right)\\ - A \cosh \left( \frac{\operatorname{Re}(\omega)}{A} \right) \sin \left( \frac{\operatorname{Im}(\omega)}{A} \right) \\ \operatorname{Re}(\omega) \\ \end{bmatrix} + \sin(\alpha) \begin{bmatrix} A \sinh \left( \frac{\operatorname{Re}(\omega)}{A} \right) \sin \left( \frac{\operatorname{Im}(\omega)}{A} \right)\\ A \sinh \left( \frac{\operatorname{Re}(\omega)}{A} \right) \cos \left( \frac{\operatorname{Im}(\omega)}{A} \right) \\ \operatorname{Im}(\omega) \\ \end{bmatrix} }[/math]

Choosing the parameters of the surface as [math]\displaystyle{ \omega = s + i(A \phi) }[/math]: [math]\displaystyle{ \mathbf{X}(s,\phi)= \cos(\alpha) \begin{bmatrix} A \cosh \left( \frac{s}{A} \right) \cos \left( \phi \right)\\ - A \cosh \left( \frac{s}{A} \right) \sin \left( \phi \right) \\ s \\ \end{bmatrix} + \sin(\alpha) \begin{bmatrix} A \sinh \left( \frac{s}{A} \right) \sin \left( \phi \right)\\ A \sinh \left( \frac{s}{A} \right) \cos \left( \phi \right) \\ A \phi \\ \end{bmatrix} }[/math]

At the extremes, the surface is a catenoid [math]\displaystyle{ (\alpha = 0) }[/math] or a helicoid [math]\displaystyle{ (\alpha = \pi/2) }[/math]. Otherwise, [math]\displaystyle{ \alpha }[/math] represents a mixing angle. The resulting surface, with domain chosen to prevent self-intersection, is a catenary rotated around the [math]\displaystyle{ \mathbf{X}_3 }[/math] axis in a helical fashion.

A catenary that spans periodic points on a helix, subsequently rotated along the helix to produce a minimal surface.

The fundamental domain (C) and the 3D surfaces. The continuous surfaces are made of copies of the fundamental patch (R3)

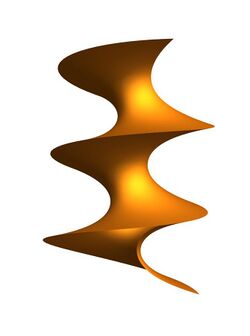
Lines of curvature

One can rewrite each element of second fundamental matrix as a function of [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math], for example [math]\displaystyle{ \mathbf{X_{uu}} \cdot \mathbf{\hat{n}} = \frac{1}{|g|^2+1} \begin{bmatrix} \operatorname{Re} \left( ( 1- g^2 ) f' - 2gfg'\right) \\ \operatorname{Re} \left( ( 1+ g^2 ) f'i+ 2gfg'i \right) \\ \operatorname{Re} \left( 2gf' +2fg' \right) \\ \end{bmatrix} \cdot \begin{bmatrix} \operatorname{Re} \left( 2g \right) \\ \operatorname{Re} \left( -2gi \right) \\ \operatorname{Re} \left( |g|^2-1 \right) \\ \end{bmatrix} = -2\operatorname{Re} (fg') }[/math]

And consequently the second fundamental form matrix can be simplified as [math]\displaystyle{ \begin{bmatrix} -\operatorname{Re} f g' & \;\; \operatorname{Im} f g' \\ \operatorname{Im} f g' & \;\; \operatorname{Re} f g' \end{bmatrix} }[/math]

Lines of curvature make a quadrangulation of the domain

One of its eigenvectors is [math]\displaystyle{ \overline{\sqrt{ f g'} } }[/math] which represents the principal direction in the complex domain. Therefore, the two principal directions in the [math]\displaystyle{ uv }[/math] space turn out to be [math]\displaystyle{ \phi = -\frac{1}{2} \operatorname{Arg}(f g') \pm k \pi /2 }[/math]

See also

• Associate family
• Bryant surface, found by an analogous parameterization in hyperbolic space