Zyablov bound

In coding theory, the Zyablov bound is a lower bound on the rate [math]\displaystyle{ r }[/math] and relative distance [math]\displaystyle{ \delta }[/math] that are achievable by concatenated codes.

Statement of the bound

The bound states that there exists a family of [math]\displaystyle{ q }[/math]-ary (concatenated, linear) codes with rate [math]\displaystyle{ r }[/math] and relative distance [math]\displaystyle{ \delta }[/math] whenever

[math]\displaystyle{ r \leqslant \max\limits_{0 \leqslant r' \leqslant 1 - H_q(\delta)} r' \cdot \left (1 - {\delta \over {H_q ^{-1}(1 - r')}} \right ) }[/math],

where [math]\displaystyle{ H_q }[/math]is the [math]\displaystyle{ q }[/math]-ary entropy function

[math]\displaystyle{ H_q(x) = x \log_q(q-1) - x \log_q(x) - (1 - x) \log_q(1 - x) }[/math].

Figure 1: The Zyablov bound. For comparison, the GV bound (which gives achievable parameters for general codes that may not be efficiently decodable) is also plotted.

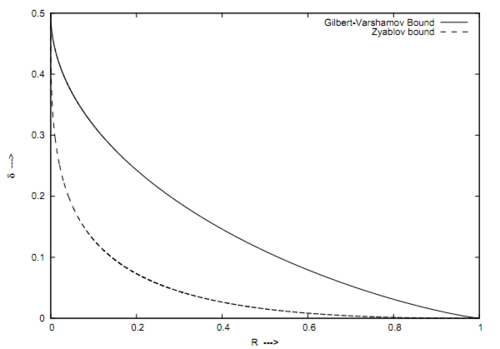
Description

The bound is obtained by considering the range of parameters that are obtainable by concatenating a "good" outer code [math]\displaystyle{ C_{out} }[/math] with a "good" inner code [math]\displaystyle{ C_{in} }[/math]. Specifically, we suppose that the outer code meets the Singleton bound, i.e. it has rate [math]\displaystyle{ r_{out} }[/math]and relative distance [math]\displaystyle{ \delta_{out} }[/math] satisfying [math]\displaystyle{ r_{out} + \delta_{out} = 1 }[/math]. Reed Solomon codes are a family of such codes that can be tuned to have any rate [math]\displaystyle{ r_{out} \in (0,1) }[/math] and relative distance [math]\displaystyle{ 1 - r_{out} }[/math] (albeit over an alphabet as large as the codeword length). We suppose that the inner code meets the Gilbert–Varshamov bound, i.e. it has rate [math]\displaystyle{ r_{in} }[/math]and relative distance [math]\displaystyle{ \delta_{in} }[/math] satisfying [math]\displaystyle{ r_{in} + H_q(\delta_{in}) \ge 1 }[/math]. Random linear codes are known to satisfy this property with high probability, and an explicit linear code satisfying the property can be found by brute-force search (which requires time polynomial in the size of the message space).

The concatenation of [math]\displaystyle{ C_{out} }[/math] and [math]\displaystyle{ C_{in} }[/math], denoted [math]\displaystyle{ C_{out} \circ C_{in} }[/math], has rate [math]\displaystyle{ r = r_{in} \cdot r_{out} }[/math] and relative distance [math]\displaystyle{ \delta = \delta_{out} \cdot \delta_{in} \ge (1 - r_{out}) \cdot H_q^{-1}(1 - r_{in}). }[/math]

Expressing [math]\displaystyle{ r_{out} }[/math] as a function of [math]\displaystyle{ \delta, r_{in} }[/math],

[math]\displaystyle{ r_{out} \ge 1- \frac{\delta}{H^{-1}(1-r_{in})} }[/math]

Then optimizing over the choice of [math]\displaystyle{ r_{in} }[/math], we see it is possible for the concatenated code to satisfy,

[math]\displaystyle{ r \ge \max\limits_{0\le r_{in} \le {1- H_q(\delta)}} r_{in} \cdot \left ( 1 - {\delta \over {H_q ^{-1}(1 - r_{in})}} \right ) }[/math]

See Figure 1 for a plot of this bound.

Note that the Zyablov bound implies that for every [math]\displaystyle{ \delta\gt 0 }[/math], there exists a (concatenated) code with positive rate and positive relative distance.

Remarks

We can construct a code that achieves the Zyablov bound in polynomial time. In particular, we can construct explicit asymptotically good code (over some alphabets) in polynomial time.

Linear Codes will help us complete the proof of the above statement since linear codes have polynomial representation. Let Cout be an [math]\displaystyle{ [N, K]_{Q} }[/math] Reed–Solomon error correction code where [math]\displaystyle{ N = Q-1 }[/math] (evaluation points being [math]\displaystyle{ \mathbb{F}_{Q}^* }[/math] with [math]\displaystyle{ Q = q^k }[/math], then [math]\displaystyle{ k = \theta(\log N) }[/math].

We need to construct the Inner code that lies on Gilbert-Varshamov bound. This can be done in two ways

1. To perform an exhaustive search on all generator matrices until the required property is satisfied for [math]\displaystyle{ C_{in} }[/math]. This is because Varshamovs bound states that there exists a linear code that lies on Gilbert-Varshamon bound which will take [math]\displaystyle{ q^{O(kn)} }[/math] time. Using [math]\displaystyle{ k=rn }[/math] we get [math]\displaystyle{ q^{O(kn)}=q^{O(k^{2})}=N^{O(\log N)} }[/math], which is upper bounded by [math]\displaystyle{ nN^{O(\log nN)} }[/math], a quasi-polynomial time bound.
2. To construct [math]\displaystyle{ C_{in} }[/math] in [math]\displaystyle{ q^{O(n)} }[/math] time and use [math]\displaystyle{ (nN)^{O(1)} }[/math] time overall. This can be achieved by using the method of conditional expectation on the proof that random linear code lies on the bound with high probability.

Thus we can construct a code that achieves the Zyablov bound in polynomial time.

See also

• Gilbert-Varshamov bound
• Singleton bound

References and external links

• MIT Lecture Notes on Essential Coding Theory – Dr. Madhu Sudan
• University at Buffalo Lecture Notes on Coding Theory – Dr. Atri Rudra
• University of Washington Lecture Notes on Coding Theory- Dr. Venkatesan Guruswami