Chemistry:Diffusion-limited enzyme

From HandWiki
Revision as of 20:43, 7 May 2022 by imported>BotanyGa (url)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Enzyme rate limited by diffusion
The distribution of known enzyme catalytic rates (kcat/KM). Most enzymes have a rate around 105 s−1M−1. The fastest enzymes in the dark box on the right (>108 s−1M−1) are constrained by the diffusion limit. (Data adapted from reference[1])

A diffusion-limited enzyme catalyses a reaction so efficiently that the rate limiting step is that of substrate diffusion into the active site, or product diffusion out.[2] This is also known as kinetic perfection or catalytic perfection. Since the rate of catalysis of such enzymes is set by the diffusion-controlled reaction, it therefore represents an intrinsic, physical constraint on evolution (a maximum peak height in the fitness landscape). Diffusion limited perfect enzymes are very rare. Most enzymes catalyse their reactions to a rate that is 1,000-10,000 times slower than this limit. This is due to both the chemical limitations of difficult reactions, and the evolutionary limitations that such high reaction rates do not confer any extra fitness.[1]

History

An illustration to show (a) Alberty-Hammes-Eigen model, and (b) Chou's model, where E denotes the enzyme whose active site is colored in red, while the substrate S in blue.

The theory of diffusion-controlled reaction was originally utilized by R.A. Alberty, Gordon Hammes, and Manfred Eigen to estimate the upper limit of enzyme-substrate reaction.[3][4] According to their estimation,[3][4] the upper limit of enzyme-substrate reaction was 109 M−1 s−1.

In 1972, it was observed that in the dehydration of H2CO3 catalyzed by carbonic anhydrase, the second-order rate constant obtained experimentally was about 1.5 × 1010 M−1 s−1,[5] which was one order of magnitude higher than the upper limit estimated by Alberty, Hammes, and Eigen based on a simplified model.[3][4]

To address such a paradox, Kuo-Chen Chou and his co-workers proposed a model by taking into account the spatial factor and force field factor between the enzyme and its substrate and found that the upper limit could reach 1010 M−1 s−1,[6][7][8] and can be used to explain some surprisingly high reaction rates in molecular biology.[5][9][10]

The new upper limit found by Chou et al. for enzyme-substrate reaction was further discussed and analyzed by a series of follow-up studies.[11][12][13]

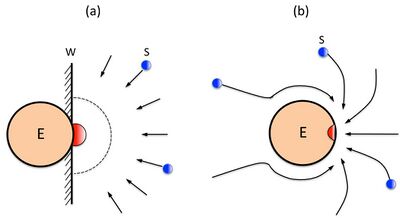
A detailed comparison between the simplified Alberty-Hammes-Eigen's model (a) and the Chou's model (b) in calculating the diffusion-controlled reaction rate of enzyme with its substrate, or the upper limit of enzyme-substrate reaction, was elaborated in the paper.[14]

Mechanism

Kinetically perfect enzymes have a specificity constant, kcat/Km, on the order of 108 to 109 M−1 s−1. The rate of the enzyme-catalysed reaction is limited by diffusion and so the enzyme 'processes' the substrate well before it encounters another molecule.[1]

Some enzymes operate with kinetics which are faster than diffusion rates, which would seem to be impossible. Several mechanisms have been invoked to explain this phenomenon. Some proteins are believed to accelerate catalysis by drawing their substrate in and preorienting them by using dipolar electric fields. Some invoke a quantum-mechanical tunneling explanation whereby a proton or an electron can tunnel through activation barriers. If the proton tunneling theory remained a controversial idea,[15][16] it has been proven to be the only possible mechanism in the case of the soybean lipoxygenase.[17]

Evolution

It is worth noting that there are not many kinetically perfect enzymes. This can be explained in terms of natural selection. An increase in catalytic speed may be favoured as it could confer some advantage to the organism. However, when the catalytic speed outstrips diffusion speed (i.e. substrates entering and leaving the active site, and also encountering substrates) there is no more advantage to increase the speed even further. The diffusion limit represents an absolute physical constraint on evolution.[1] Increasing the catalytic speed past the diffusion speed will not aid the organism in any way and so represents a global maximum in a fitness landscape. Therefore, these perfect enzymes must have come about by 'lucky' random mutation which happened to spread, or because the faster speed was once useful as part of a different reaction in the enzyme's ancestry.[citation needed]

Examples

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 Bar-Even, Arren; Noor, Elad; Savir, Yonatan; Liebermeister, Wolfram; Davidi, Dan; Tawfik, Dan S; Milo, Ron (2011). "The Moderately Efficient Enzyme: Evolutionary and Physicochemical Trends Shaping Enzyme Parameters". Biochemistry 50 (21): 4402–10. doi:10.1021/bi2002289. PMID 21506553. 
  2. ↑ Berg, Jeremy M.; Tymoczko, J. L.; Stryer, L. (2006). "Oxidative phosphorylation". Biochemistry (5 ed.). pp. 491–526. ISBN 978-0716787242. 
  3. ↑ 3.0 3.1 3.2 Alberty, Robert A.; Hammes, Gordon G. (1958). "Application of the Theory of Diffusion-controlled Reactions to Enzyme Kinetics". Journal of Physical Chemistry 62 (2): 154–9. doi:10.1021/j150560a005. 
  4. ↑ 4.0 4.1 4.2 Eigen, Manfred; Hammes, Gordon G. (2006). "Elementary Steps in Enzyme Reactions (as Studied by Relaxation Spectrometry)". in Nord, F. F.. Advances in Enzymology and Related Areas of Molecular Biology. 25. 1–38. doi:10.1002/9780470122709.ch1. ISBN 978-0-470-12270-9. OCLC 777630506. 
  5. ↑ 5.0 5.1 Koenig, Seymour H.; Brown, Rodney D. (1972). "H2CO3 as Substrate for Carbonic Anhydrase in the Dehydration of HCO3−". Proceedings of the National Academy of Sciences of the United States of America 69 (9): 2422–5. doi:10.1073/pnas.69.9.2422. PMID 4627028. Bibcode: 1972PNAS...69.2422K. 
  6. ↑ Chou, Kuo-Chen; Jiang, Shou-Ping (1974). "Studies on the rate of diffusion-controlled reactions of enzymes. Spatial factor and force field factor". Scientia Sinica 27 (5): 664–80. PMID 4219062. 
  7. ↑ Chou, Kuo-Chen (1976). "The kinetics of the combination reaction between enzyme and substrate". Scientia Sinica 19 (4): 505–28. PMID 824728. 
  8. ↑ Li, TT; Chou, KC (1976). "The quantitative relations between diffusion-controlled reaction rate and characteristic parameters in enzyme-substrate reaction systems. I. Neutral substrates". Scientia Sinica 19 (1): 117–36. PMID 1273571. 
  9. ↑ Riggs, Arthur D; Bourgeois, Suzanne; Cohn, Melvin (1970). "The lac represser-operator interaction". Journal of Molecular Biology 53 (3): 401–17. doi:10.1016/0022-2836(70)90074-4. PMID 4924006. 
  10. ↑ Kirschner, Kasper; Gallego, Ernesto; Schuster, Inge; Goodall, David (1971). "Co-operative binding of nicotinamide-adenine dinucleotide to yeast glyceraldehyde-3-phosphate dehydrogenase". Journal of Molecular Biology 58 (1): 29–50. doi:10.1016/0022-2836(71)90230-0. PMID 4326080. 
  11. ↑ Chou, Kuo Chen; Zhou, Guo Ping (1982). "Role of the protein outside active site on the diffusion-controlled reaction of enzymes". Journal of the American Chemical Society 104 (5): 1409–1413. doi:10.1021/ja00369a043. 
  12. ↑ Payens, T.A.J (1983). "Why are enzymes so large?". Trends in Biochemical Sciences 8 (2): 46. doi:10.1016/0968-0004(83)90382-1. 
  13. ↑ Zhou, Guozhi; Wong, Ming-Tat; Zhou, Guo-Qiang (1983). "Diffusion-controlled reactions of enzymes". Biophysical Chemistry 18 (2): 125–32. doi:10.1016/0301-4622(83)85006-6. PMID 6626685. 
  14. ↑ Zhou, Guo-Qiang; Zhong, Wei-Zhu (1982). "Diffusion-Controlled Reactions of Enzymes". European Journal of Biochemistry 128 (2–3): 383–7. doi:10.1111/j.1432-1033.1982.tb06976.x. PMID 7151785. 
  15. ↑ Garcia-Viloca, M; Gao, Jiali; Karplus, Martin; Truhlar, Donald G (2004). "How Enzymes Work: Analysis by Modern Rate Theory and Computer Simulations". Science 303 (5655): 186–95. doi:10.1126/science.1088172. PMID 14716003. Bibcode: 2004Sci...303..186G. 
  16. ↑ Olsson, Mats H. M.; Siegbahn, Per E. M.; Warshel, Arieh (2004). "Simulations of the Large Kinetic Isotope Effect and the Temperature Dependence of the Hydrogen Atom Transfer in Lipoxygenase". Journal of the American Chemical Society 126 (9): 2820–8. doi:10.1021/ja037233l. PMID 14995199. 
  17. ↑ Jevtic, S; Anders, J (2017). "A qualitative quantum rate model for hydrogen transfer in soybean lipoxygenase". The Journal of Chemical Physics 147 (11): 114108. doi:10.1063/1.4998941. PMID 28938801. Bibcode: 2017JChPh.147k4108J. 
  18. ↑ Domnik, Lilith; Merrouch, Meriem; Goetzl, Sebastian; Jeoung, Jae-Hun; Léger, Christophe; Dementin, Sébastien; Fourmond, Vincent; Dobbek, Holger (2017-11-27). "CODH-IV: A High-Efficiency CO-Scavenging CO Dehydrogenase with Resistance to O2" (in en). Angewandte Chemie International Edition 56 (48): 15466–15469. doi:10.1002/anie.201709261. ISSN 1521-3773. PMID 29024326. https://hal.archives-ouvertes.fr/hal-01696167/file/2017_05_18_CODH4_AC%2BCL%2BMM%2BVF.pdf. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Chemistry:Diffusion-limited_enzyme&oldid=110425"