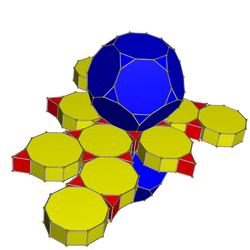
Truncated dodecahedral prism
From HandWiki
Revision as of 00:58, 10 May 2022 by imported>Raymond Straus (url)
Short description: Convex uniform polychoron
| Truncated dodecahedral prism | |
|---|---|
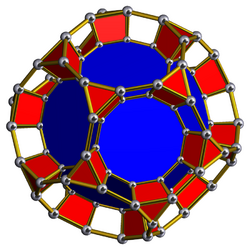 Schlegel diagram Decagonal prisms hidden | |
| Type | Prismatic uniform polychoron |
| Uniform index | 60 |
| Schläfli symbol | t0,1,3{3,5,2} or t{3,5}×{} |
| Coxeter-Dynkin |     
|
| Cells | 34 total: 2 t0,1{5,3} 12 {}x{10} 20 {}x{3} |
| Faces | 154 total: 40 {3} 90 {4} 24 {10} |
| Edges | 240 |
| Vertices | 120 |
| Vertex figure | 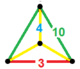 Isosceles-triangular pyramid |
| Symmetry group | [5,3,2], order 240 |
| Properties | convex |
In geometry, a truncated dodecahedral prism is a convex uniform polychoron (four-dimensional polytope).
It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.
Alternative names
- Truncated-dodecahedral dyadic prism (Norman W. Johnson)
- Tiddip (Jonathan Bowers: for truncated-dodecahedral prism)
- Truncated-dodecahedral hyperprism
See also
- Truncated 120-cell,
External links
- 6. Convex uniform prismatic polychora - Model 60, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x o3x5x - tiddip". https://bendwavy.org/klitzing/dimensions/polychora.htm.
 |  |
