Decagon

Short description: Shape with ten sides

Regular decagon
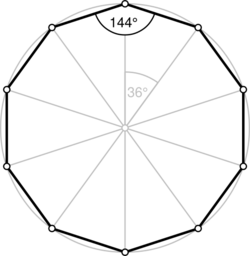A regular decagon
Type	Regular polygon
Edges and vertices	10
Schläfli symbol	{10}, t{5}
Coxeter diagram
Symmetry group	Dihedral (D10), order 2×10
Internal angle (degrees)	144°
Dual polygon	Self
Properties	Convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a decagon (from the Greek δέκα déka and γωνία gonía, "ten angles") is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.

Regular decagon

A regular decagon has all sides of equal length and each internal angle will always be equal to 144°. Its Schläfli symbol is {10} and can also be constructed as a truncated pentagon, t{5}, a quasiregular decagon alternating two types of edges.

Side length

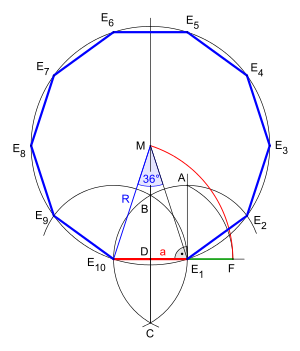
The picture shows a regular decagon with side length [math]\displaystyle{ a }[/math] and radius [math]\displaystyle{ R }[/math] of the circumscribed circle.

• The triangle [math]\displaystyle{ E_{10}E_1M }[/math] has two equally long legs with length [math]\displaystyle{ R }[/math] and a base with length [math]\displaystyle{ a }[/math]
• The circle around [math]\displaystyle{ E_1 }[/math] with radius [math]\displaystyle{ a }[/math] intersects [math]\displaystyle{ ]M\,E_{10}[ }[/math] in a point [math]\displaystyle{ P }[/math] (not designated in the picture).
• Now the triangle [math]\displaystyle{ {E_{10}E_1P}\; }[/math] is an isosceles triangle with vertex [math]\displaystyle{ E_1 }[/math] and with base angles [math]\displaystyle{ m\angle E_1 E_{10} P = m\angle E_{10} P E_1 = 72^\circ \; }[/math].
• Therefore [math]\displaystyle{ m\angle P E_1 E_{10} = 180^\circ -2\cdot 72^\circ = 36^\circ \; }[/math]. So [math]\displaystyle{ \; m\angle M E_1 P = 72^\circ- 36^\circ = 36^\circ\; }[/math] and hence [math]\displaystyle{ \; E_1 M P\; }[/math] is also an isosceles triangle with vertex [math]\displaystyle{ P }[/math]. The length of its legs is [math]\displaystyle{ a }[/math], so the length of [math]\displaystyle{ [P\,E_{10}] }[/math] is [math]\displaystyle{ R-a }[/math].
• The isosceles triangles [math]\displaystyle{ E_{10} E_1 M\; }[/math] and [math]\displaystyle{ P E_{10} E_1\; }[/math] have equal angles of 36° at the vertex, and so they are similar, hence: [math]\displaystyle{ \;\frac{a}{R}=\frac{R-a}{a} }[/math]
• Multiplication with the denominators [math]\displaystyle{ R,a \gt 0 }[/math] leads to the quadratic equation: [math]\displaystyle{ \;a^2=R^2-aR\; }[/math]
• This equation for the side length [math]\displaystyle{ a\, }[/math] has one positive solution: [math]\displaystyle{ \;a=\frac{R}{2}(-1+\sqrt{5}) }[/math]

So the regular decagon can be constructed with ruler and compass.

Further conclusions

[math]\displaystyle{ \;R=\frac{2a}{\sqrt{5}-1}=\frac{a}{2}(\sqrt{5}+1)\; }[/math] and the base height of [math]\displaystyle{ \Delta\,E_{10} E_1 M\, }[/math] (i.e. the length of [math]\displaystyle{ [M\,D] }[/math]) is [math]\displaystyle{ h = \sqrt{R^2-(a/2)^2}=\frac{a}{2}\sqrt{5+2\sqrt{5}}\; }[/math] and the triangle has the area: [math]\displaystyle{ A_\Delta=\frac{a}{2}\cdot h = \frac{a^2}{4}\sqrt{5+2\sqrt{5}} }[/math].

Area

The area of a regular decagon of side length a is given by:

[math]\displaystyle{ A = \frac{5}{2} a^2\cot\left(\frac{\pi}{10} \right) = \frac{5}{2} a^2\sqrt{5+2\sqrt{5}} \simeq 7.694208843\,a^2 }[/math]

In terms of the apothem r (see also inscribed figure), the area is:

[math]\displaystyle{ A = 10 \tan\left(\frac{\pi}{10}\right) r^2 = 2r^2\sqrt{5\left(5-2\sqrt5\right)} \simeq 3.249196962\,r^2 }[/math]

In terms of the circumradius R, the area is:

[math]\displaystyle{ A = 5 \sin\left(\frac{\pi}{5}\right) R^2 = \frac{5}{2}R^2\sqrt{\frac{5-\sqrt{5}}{2}} \simeq 2.938926261\,R^2 }[/math]

An alternative formula is [math]\displaystyle{ A=2.5da }[/math] where d is the distance between parallel sides, or the height when the decagon stands on one side as base, or the diameter of the decagon's inscribed circle. By simple trigonometry,

[math]\displaystyle{ d=2a\left(\cos\tfrac{3\pi}{10}+\cos\tfrac{\pi}{10}\right), }[/math]

and it can be written algebraically as

[math]\displaystyle{ d=a\sqrt{5+2\sqrt{5}}. }[/math]

Sides

A regular decagon has 10 sides and is equilateral. It has 35 diagonals

Construction

As 10 = 2 × 5, a power of two times a Fermat prime, it follows that a regular decagon is constructible using compass and straightedge, or by an edge-bisection of a regular pentagon.

Construction of decagon

Construction of pentagon

An alternative (but similar) method is as follows:

1. Construct a pentagon in a circle by one of the methods shown in constructing a pentagon.
2. Extend a line from each vertex of the pentagon through the center of the circle to the opposite side of that same circle. Where each line cuts the circle is a vertex of the decagon.  In other words,  the image of a regular pentagon under a point reflection with respect of its center is a concentric congruent pentagon,  and the two pentagons have in total the vertices of a concentric regular decagon.
3. The five corners of the pentagon constitute alternate corners of the decagon. Join these points to the adjacent new points to form the decagon.

Nonconvex regular decagon

This tiling by golden triangles, a regular pentagon, contains a stellation of regular decagon, the Schäfli symbol of which is {10/3}.

The length ratio of two inequal edges of a golden triangle is the golden ratio, denoted by [math]\displaystyle{ \Phi }[/math], or its multiplicative inverse: [math]\displaystyle{ \Phi - 1 = \frac{1}{\Phi} = 2\,\cos 72\,^\circ = \frac{1}{\,2\,\cos 36\,^\circ} = \frac{\,\sqrt{5} - 1\,}{2} \text{.} }[/math] So we can get the properties of a regular decagonal star, through a tiling by golden triangles that fills this star polygon.

The golden ratio in decagon

Both in the construction with given circumcircle as well as with given side length is the golden ratio dividing a line segment by exterior division the determining construction element.

• In the construction with given circumcircle the circular arc around G with radius GE₃ produces the segment AH, whose division corresponds to the golden ratio.

[math]\displaystyle{ \frac{\overline{AM}}{\overline{MH}} = \frac{\overline{AH}}{\overline{AM}} = \frac{1+ \sqrt{5}}{2} = \Phi \approx 1.618 \text{.} }[/math]

• In the construction with given side length the circular arc around D with radius DA produces the segment E₁₀F, whose division corresponds to the golden ratio.

[math]\displaystyle{ \frac{\overline{E_1 E_{10}}}{\overline{E_1 F}} = \frac{\overline{E_{10} F}}{\overline{E_1 E_{10}}} = \frac{R}{a} = \frac{1+ \sqrt{5}}{2} =\Phi \approx 1.618 \text{.} }[/math]

Decagon with given circumcircle, animation

Decagon with a given side length, animation

Symmetry

Symmetries of a regular decagon. Vertices are colored by their symmetry positions. Blue mirrors are drawn through vertices, and purple mirrors are drawn through edges. Gyration orders are given in the center.

The regular decagon has Dih₁₀ symmetry, order 20. There are 3 subgroup dihedral symmetries: Dih₅, Dih₂, and Dih₁, and 4 cyclic group symmetries: Z₁₀, Z₅, Z₂, and Z₁.

These 8 symmetries can be seen in 10 distinct symmetries on the decagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order. Full symmetry of the regular form is r20 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g10 subgroup has no degrees of freedom but can be seen as directed edges.

The highest symmetry irregular decagons are d10, an isogonal decagon constructed by five mirrors which can alternate long and short edges, and p10, an isotoxal decagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular decagon.

Dissection

10-cube projection	40 rhomb dissection

Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms. In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular decagon, m=5, and it can be divided into 10 rhombs, with examples shown below. This decomposition can be seen as 10 of 80 faces in a Petrie polygon projection plane of the 5-cube. A dissection is based on 10 of 30 faces of the rhombic triacontahedron. The list OEIS: A006245 defines the number of solutions as 62, with 2 orientations for the first symmetric form, and 10 orientations for the other 6.

Regular decagon dissected into 10 rhombi

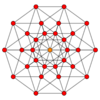5-cube

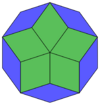
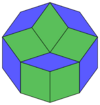
Skew decagon

3 regular skew zig-zag decagons

{5}#{ }	{5/2}#{ }	{5/3}#{ }
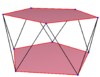
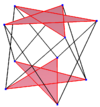
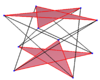
A regular skew decagon is seen as zig-zagging edges of a pentagonal antiprism, a pentagrammic antiprism, and a pentagrammic crossed-antiprism.

A skew decagon is a skew polygon with 10 vertices and edges but not existing on the same plane. The interior of such a decagon is not generally defined. A skew zig-zag decagon has vertices alternating between two parallel planes.

A regular skew decagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew decagon and can be seen in the vertices and side edges of a pentagonal antiprism, pentagrammic antiprism, and pentagrammic crossed-antiprism with the same D_5d, [2⁺,10] symmetry, order 20.

These can also be seen in these four convex polyhedra with icosahedral symmetry. The polygons on the perimeter of these projections are regular skew decagons.

Orthogonal projections of polyhedra on 5-fold axes

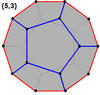Dodecahedron

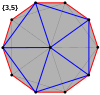Icosahedron

Icosidodecahedron

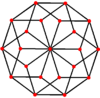Rhombic triacontahedron

Petrie polygons

The regular skew decagon is the Petrie polygon for many higher-dimensional polytopes, shown in these orthogonal projections in various Coxeter planes: The number of sides in the Petrie polygon is equal to the Coxeter number, h, for each symmetry family.

A9	D6		B5
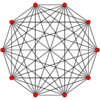9-simplex	411	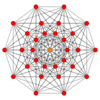131	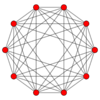5-orthoplex	5-cube

See also

• Decagonal number and centered decagonal number, figurate numbers modeled on the decagon
• Decagram, a star polygon with the same vertex positions as the regular decagon

External links

• Weisstein, Eric W.. "Decagon". http://mathworld.wolfram.com/Decagon.html. 
• Definition and properties of a decagon With interactive animation