Bimonster group

In mathematics, the bimonster is a group that is the wreath product of the monster group M with Z₂:

[math]\displaystyle{ Bi = M \wr \mathbb{Z}_2. \, }[/math]

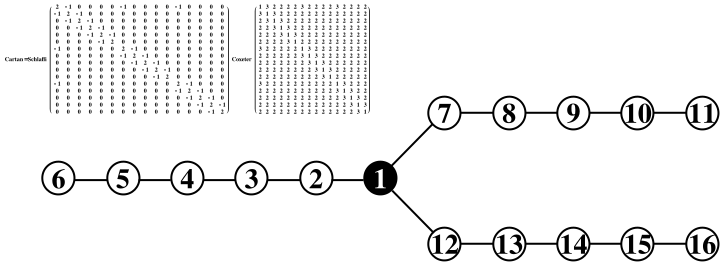
The Bimonster is also a quotient of the Coxeter group corresponding to the Dynkin diagram Y₅₅₅, a Y-shaped graph with 16 nodes:

John H. Conway conjectured that a presentation of the bimonster could be given by adding a certain extra relation to the presentation defined by the Y₅₅₅ diagram; this was proved in 1990 by A. A. Ivanov a mathematician not the famous painter and Simon P. Norton.

See also

• Triality - simple Lie group D₄, Y₁₁₁
• Affine E 6 Y₂₂₂

References

• Basak, Tathagata (2007), "The complex Lorentzian Leech lattice and the Bimonster", Journal of Algebra 309 (1): 32–56, doi:10.1016/j.jalgebra.2006.05.033 .
• "The Bimonster, the group Y₅₅₅, and the projective plane of order 3", Computers in Algebra (Chicago, IL, 1985), Lecture Notes in Pure and Applied Mathematics, 111, New York: Dekker, 1988, pp. 27–50 .
• "Hyperbolic reflections for the Bimonster and 3Fi₂₄", Groups, Combinatorics & Geometry (Durham, 1990), London Math. Soc. Lecture Note Ser., 165, Cambridge: Cambridge University Press, 1992, pp. 24–45, doi:10.1017/CBO9780511629259.006 .
• "26 implies the Bimonster", Journal of Algebra 235 (2): 805–814, 2001, doi:10.1006/jabr.2000.8494 .
• Simons, Christopher Smyth (1997), Hyperbolic reflection groups, completely replicable functions, the Monster and the Bimonster, Ph.D. thesis, Princeton University, Department of Mathematics, ISBN 978-0591-50546-7 .
• Soicher, Leonard H. (1989), "From the Monster to the Bimonster", Journal of Algebra 121 (2): 275–280, doi:10.1016/0021-8693(89)90064-1 .

External links

• Weisstein, Eric W.. "Bimonster". http://mathworld.wolfram.com/Bimonster.html.  (Note: incorrectly named here as [3^6,6,6])