Monster group

From HandWiki
Short description: Finite simple group
Algebraic structure → Group theory
Group theory
Cyclic group.svg
Basic notions
Group homomorphisms
Finite groups
Classification of finite simple groups
Modular groups
  • PSL(2,Z)
  • SL(2,Z)
Topological and Lie groups
Infinite dimensional Lie group
  • O(∞)
  • SU(∞)
  • Sp(∞)
Algebraic groups

In the area of abstract algebra known as group theory, the monster group M (also known as the Fischer–Griess monster, or the friendly giant) is the largest sporadic simple group, having order
      246 · 320 · 59 · 76 · 112 · 133 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71
   = 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000
   ≈ 8×1053.

The finite simple groups have been completely classified. Every such group belongs to one of 18 countably infinite families or is one of 26 sporadic groups that do not follow such a systematic pattern. The monster group contains 20 sporadic groups (including itself) as subquotients. Robert Griess, who proved the existence of the monster in 1982, has called those 20 groups the happy family, and the remaining six exceptions pariahs.

It is difficult to give a good constructive definition of the monster because of its complexity. Martin Gardner wrote a popular account of the monster group in his June 1980 Mathematical Games column in Scientific American.[1]

History

The monster was predicted by Bernd Fischer (unpublished, about 1973) and Robert Griess[2] as a simple group containing a double cover of Fischer's baby monster group as a centralizer of an involution. Within a few months, the order of M was found by Griess using the Thompson order formula, and Fischer, Conway, Norton and Thompson discovered other groups as subquotients, including many of the known sporadic groups, and two new ones: the Thompson group and the Harada–Norton group. The character table of the monster, a 194-by-194 array, was calculated in 1979 by Fischer and Donald Livingstone using computer programs written by Michael Thorne. It was not clear in the 1970s whether the monster actually existed. Griess[3] constructed M as the automorphism group of the Griess algebra, a 196,884-dimensional commutative nonassociative algebra over the real numbers; he first announced his construction in Ann Arbor on January 14, 1980. In his 1982 paper, he referred to the monster as the Friendly Giant, but this name has not been generally adopted. John Conway[4] and Jacques Tits[5][6] subsequently simplified this construction.

Griess's construction showed that the monster exists. Thompson[7] showed that its uniqueness (as a simple group satisfying certain conditions coming from the classification of finite simple groups) would follow from the existence of a 196,883-dimensional faithful representation. A proof of the existence of such a representation was announced by Norton,[8] though he never published the details. Griess, Meierfrankenfeld, and Segev gave the first complete published proof of the uniqueness of the monster (more precisely, they showed that a group with the same centralizers of involutions as the monster is isomorphic to the monster).[9]

The monster was a culmination of the development of sporadic simple groups and can be built from any two of three subquotients: the Fischer group Fi24, the baby monster, and the Conway group Co1.

The Schur multiplier and the outer automorphism group of the monster are both trivial.

Representations

The minimal degree of a faithful complex representation is 47 × 59 × 71 = 196,883, hence is the product of the three largest prime divisors of the order of M. The smallest faithful linear representation over any field has dimension 196,882 over the field with two elements, only one less than the dimension of the smallest faithful complex representation.

The smallest faithful permutation representation of the monster is on 24 · 37 · 53 · 74 · 11 · 132 · 29 · 41 · 59 · 71 (about 1020) points.

The monster can be realized as a Galois group over the rational numbers,[10] and as a Hurwitz group.[11]

The monster is unusual among simple groups in that there is no known easy way to represent its elements. This is not due so much to its size as to the absence of "small" representations. For example, the simple groups A100 and SL20(2) are far larger but easy to calculate with as they have "small" permutation or linear representations. Alternating groups, such as A100, have permutation representations that are "small" compared to the size of the group, and all finite simple groups of Lie type, such as SL20(2), have linear representations that are "small" compared to the size of the group. All sporadic groups other than the monster also have linear representations small enough that they are easy to work with on a computer (the next hardest case after the monster is the baby monster, with a representation of dimension 4370).

Computer construction

Martin Seysen has implemented a fast Python package named mmgroup, which claims to be the first implementation of the monster group where arbitrary operations can effectively be performed. The documentation states that multiplication of group elements takes less than 40 milliseconds on a typical modern PC, which is five orders of magnitude faster than estimated by Robert A. Wilson in 2013.[12][13][14][15] The mmgroup software package has been used to find two new maximal subgroups of the monster group.[16]

Previously, Robert A. Wilson had found explicitly (with the aid of a computer) two invertible 196,882 by 196,882 matrices (with elements in the field of order 2) which together generate the monster group by matrix multiplication; this is one dimension lower than the 196,883-dimensional representation in characteristic 0. Performing calculations with these matrices was possible but is too expensive in terms of time and storage space to be useful, as each such matrix occupies over four and a half gigabytes.[17]

Wilson asserts that the best description of the monster is to say, "It is the automorphism group of the monster vertex algebra". This is not much help however, because nobody has found a "really simple and natural construction of the monster vertex algebra".[18]

Wilson with collaborators found a method of performing calculations with the monster that was considerably faster, although now superseded by Seysen's abovementioned work. Let V be a 196,882 dimensional vector space over the field with 2 elements. A large subgroup H (preferably a maximal subgroup) of the Monster is selected in which it is easy to perform calculations. The subgroup H chosen is 31+12.2.Suz.2, where Suz is the Suzuki group. Elements of the monster are stored as words in the elements of H and an extra generator T. It is reasonably quick to calculate the action of one of these words on a vector in V. Using this action, it is possible to perform calculations (such as the order of an element of the monster). Wilson has exhibited vectors u and v whose joint stabilizer is the trivial group. Thus (for example) one can calculate the order of an element g of the monster by finding the smallest i > 0 such that giu = u and giv = v. This and similar constructions (in different characteristics) were used to find some of the non-local maximal subgroups of the monster group.

Moonshine

Main page: Monstrous moonshine

The monster group is one of two principal constituents in the monstrous moonshine conjecture by Conway and Norton,[19] which relates discrete and non-discrete mathematics and was finally proved by Richard Borcherds in 1992.

In this setting, the monster group is visible as the automorphism group of the monster module, a vertex operator algebra, an infinite dimensional algebra containing the Griess algebra, and acts on the monster Lie algebra, a generalized Kac–Moody algebra.

Many mathematicians, including Conway, have seen the monster as a beautiful and still mysterious object.[20] Conway said of the monster group: "There's never been any kind of explanation of why it's there, and it's obviously not there just by coincidence. It's got too many intriguing properties for it all to be just an accident."[21] Simon P. Norton, an expert on the properties of the monster group, is quoted as saying, "I can explain what Monstrous Moonshine is in one sentence, it is the voice of God."[22]

McKay's E8 observation

There are also connections between the monster and the extended Dynkin diagrams [math]\displaystyle{ \tilde E_8, }[/math] specifically between the nodes of the diagram and certain conjugacy classes in the monster, known as McKay's E8 observation.[23][24][25] This is then extended to a relation between the extended diagrams [math]\displaystyle{ \tilde E_6, \tilde E_7, \tilde E_8 }[/math] and the groups 3.Fi24′, 2.B, and M, where these are (3/2/1-fold central extensions) of the Fischer group, baby monster group, and monster. These are the sporadic groups associated with centralizers of elements of type 1A, 2A, and 3A in the monster, and the order of the extension corresponds to the symmetries of the diagram. See ADE classification: trinities for further connections (of McKay correspondence type), including (for the monster) with the rather small simple group PSL(2,11) and with the 120 tritangent planes of a canonic sextic curve of genus 4 known as Bring's curve.

Maximal subgroups

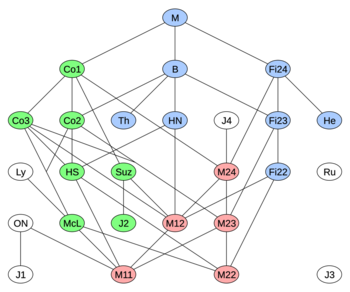
Diagram of the 26 sporadic simple groups, showing subquotient relationships.

The monster has 46 conjugacy classes of maximal subgroups.[16] Non-abelian simple groups of some 60 isomorphism types are found as subgroups or as quotients of subgroups. The largest alternating group represented is A12. The monster contains 20 of the 26 sporadic groups as subquotients. This diagram, based on one in the book Symmetry and the Monster by Mark Ronan, shows how they fit together.[26] The lines signify inclusion, as a subquotient, of the lower group by the upper one. The circled symbols denote groups not involved in larger sporadic groups. For the sake of clarity redundant inclusions are not shown.

The 46 classes of maximal subgroups of the monster are given by the following list. Previous unpublished work of Wilson et. al had purported to rule out any almost simple subgroups with non-abelian simple socles of the form U3(4), L2(8), and L2(16).[27][28][29] However, the latter was contradicted by Dietrich et al., who found a new maximal subgroup of the form U3(4). The same authors had previously found a new maximal subgroup of the form L2(13) and confirmed that there are no maximal subgroups with socle L2(8) or L2(16), thus completing the classification in the literature.[16]

Note that tables of maximal subgroups have often been found to contain subtle errors, and in particular at least two of the subgroups on the list below were incorrectly omitted from some previous lists.


  • 2.B   centralizer of an involution; contains the normalizer (47:23) × 2 of a Sylow 47-subgroup
  • 21+24.Co1   centralizer of an involution
  • 3.Fi24   normalizer of a subgroup of order 3; contains the normalizer ((29:14) × 3).2 of a Sylow 29-subgroup
  • 22.2E6(22):S3   normalizer of a Klein 4-group
  • 210+16.O10+(2)
  • 22+11+22.(M24 × S3)   normalizer of a Klein 4-group; contains the normalizer (23:11) × S4 of a Sylow 23-subgroup
  • 31+12.2Suz.2   normalizer of a subgroup of order 3
  • 25+10+20.(S3 × L5(2))
  • S3 × Th   normalizer of a subgroup of order 3; contains the normalizer (31:15) × S3 of a Sylow 31-subgroup
  • 23+6+12+18.(L3(2) × 3S6)
  • 38.O8− (3).23
  • (D10 × HN).2   normalizer of a subgroup of order 5
  • (32:2 × O8+(3)).S4
  • 32+5+10.(M11 × 2S4)
  • 33+2+6+6:(L3(3) × SD16)
  • 51+6:2J2:4   normalizer of a subgroup of order 5
  • (7:3 × He):2   normalizer of a subgroup of order 7
  • (A5 × A12):2
  • 53+3.(2 × L3(5))
  • (A6 × A6 × A6).(2 × S4)
  • (A5 × U3(8):31):2   contains the normalizer ((19:9) × A5):2 of a Sylow 19-subgroup
  • 52+2+4:(S3 × GL2(5))
  • (L3(2) × S4(4):2).2   contains the normalizer ((17:8) × L3(2)).2 of a Sylow 17-subgroup
  • 71+4:(3 × 2S7)   normalizer of a subgroup of order 7
  • (52:4.22 × U3(5)).S3
  • (L2(11) × M12):2   contains the normalizer (11:5 × M12):2 of a subgroup of order 11
  • (A7 × (A5 × A5):22):2
  • 54:(3 × 2L2(25)):22
  • 72+1+2:GL2(7)
  • M11 × A6.22
  • (S5 × S5 × S5):S3
  • (L2(11) × L2(11)):4
  • 132:2L2(13).4
  • (72:(3 × 2A4) × L2(7)):2
  • (13:6 × L3(3)).2   normalizer of a subgroup of order 13
  • 131+2:(3 × 4S4)   normalizer of a subgroup of order 13; normalizer of a Sylow 13-subgroup
  • U3(4):4  [16]
  • L2(71)   contains the normalizer 71:35 of a Sylow 71-subgroup[30]
  • L2(59)   contains the normalizer 59:29 of a Sylow 59-subgroup[31]
  • 112:(5 × 2A5)   normalizer of a Sylow 11-subgroup.
  • L2(41)   Norton and Wilson found a maximal subgroup of this form; due to a subtle error pointed out by Zavarnitsine some previous lists and papers stated that no such maximal subgroup existed[28]
  • L2(29):2  [32]
  • 72:SL2(7)   this was accidentally omitted from some previous lists of 7-local subgroups
  • L2(19):2  [30]
  • L2(13):2  [16]
  • 41:40   normalizer of a Sylow 41-subgroup


See also

Citations

  1. ↑ Gardner 1980, pp. 20–33.
  2. ↑ Griess 1976, pp. 113–118.
  3. ↑ Griess 1982, pp. 1–102.
  4. ↑ Conway 1985, pp. 513–540.
  5. ↑ Tits 1983, pp. 105–122.
  6. ↑ Tits 1984, pp. 491–499.
  7. ↑ Thompson 1979, pp. 340–346.
  8. ↑ Norton 1985, pp. 271–285.
  9. ↑ Griess, Meierfrankenfeld & Segev 1989, pp. 567–602.
  10. ↑ Thompson 1984, p. 443.
  11. ↑ Wilson 2001, pp. 367–374.
  12. ↑ Seysen, Martin. "The mmgroup API reference". https://mmgroup.readthedocs.io/en/latest/api.html. 
  13. ↑ Seysen, Martin (8 Mar 2022). "A fast implementation of the Monster group". arXiv:2203.04223 [math.GR].
  14. ↑ Seysen, Martin (13 May 2020). "A computer-friendly construction of the monster". arXiv:2002.10921 [math.GR].
  15. ↑ Wilson, Robert A. (18 Oct 2013). "The Monster and black-box groups". arXiv:1310.5016 [math.GR].
  16. ↑ 16.0 16.1 16.2 16.3 16.4 Dietrich, Lee & Popiel 2023.
  17. ↑ Borcherds 2002, p. 1076.
  18. ↑ Borcherds 2002, p. 1077.
  19. ↑ Conway & Norton 1979, pp. 308–339.
  20. ↑ Roberts 2013.
  21. ↑ Haran 2014, 7:57.
  22. ↑ Masters 2019.
  23. ↑ Duncan 2008.
  24. ↑ le Bruyn 2009.
  25. ↑ He & McKay 2015.
  26. ↑ Ronan 2006.
  27. ↑ Wilson 2010, pp. 393–403.
  28. ↑ 28.0 28.1 Norton & Wilson 2013, pp. 943–962.
  29. ↑ Wilson 2016, pp. 355–364.
  30. ↑ 30.0 30.1 Holmes & Wilson 2008, pp. 2653–2667.
  31. ↑ Holmes & Wilson 2004, pp. 141–152.
  32. ↑ Holmes & Wilson 2002, pp. 435–447.

Sources

Further reading

  • Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; Wilson, R. A. (1985). Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. with computational assistance from J. G. Thackray. Oxford University Press. ISBN 978-019853199-9. 
  • Harada, Koichiro (2001). "Mathematics of the Monster". Sugaku Expositions 14 (1): 55–71. 
  • Holmes, P. E.; Wilson, R. A. (2003). "A computer construction of the Monster using 2-local subgroups". Journal of the London Mathematical Society 67 (2): 346–364. doi:10.1112/S0024610702003976. 
  • Holmes, Petra E. (2008). "A classification of subgroups of the Monster isomorphic to S4 and an application". Journal of Algebra 319 (8): 3089–3099. doi:10.1016/j.jalgebra.2004.01.031. 
  • Ivanov, A.A. (2009). The Monster Group and Majorana Involutions. Cambridge tracts in mathematics. 176. Cambridge University Press. doi:10.1017/CBO9780511576812. ISBN 978-052188994-0. https://doi.org/10.1017/CBO9780511576812. 
  • Norton, Simon P. (1998). "Anatomy of the Monster. I". The atlas of finite groups: ten years on (Birmingham, 1995). London Math. Soc. Lecture Note Ser.. 249. Cambridge University Press. pp. 198–214. doi:10.1017/CBO9780511565830.020. ISBN 978-052157587-4. 
  • Norton, Simon P.; Wilson, Robert A. (2002). "Anatomy of the Monster. II". Proceedings of the London Mathematical Society. Third Series 84 (3): 581–598. doi:10.1112/S0024611502013357. 
  • du Sautoy, Marcus (2008). Finding Moonshine. Fourth Estate. ISBN 978-000721461-7.  published in the US by HarperCollins as Symmetry, ISBN 978-006078940-4).
  • Wilson, R. A.; Walsh, P. G.; Parker, R. A.; Linton, S. A. (1998). "Computer construction of the Monster". Journal of Group Theory 1 (4): 307–337. doi:10.1515/jgth.1998.023. 
  • McKay, John; He, Yang-Hui (2022). "Kashiwa Lectures on "New Approaches to the Monster"". Notices of the ICCM. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Monster_group&oldid=3384018"