Catalan's minimal surface
From HandWiki
Revision as of 07:33, 21 December 2020 by imported>Rtextdoc (update)
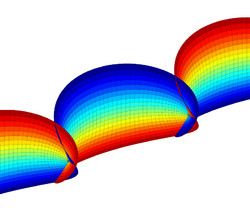
In differential geometry, Catalan's minimal surface is a minimal surface originally studied by Eugène Charles Catalan in 1855.[1]
It has the special property of being the minimal surface that contains a cycloid as a geodesic. It is also swept out by a family of parabolae.[2]
The surface has the mathematical characteristics exemplified by the following parametric equation:[3]
- [math]\displaystyle{ \begin{align} x(u,v) &= u - \sin(u)\cosh(v)\\ y(u,v) &= 1 - \cos(u)\cosh(v)\\ z(u,v) &= 4 \sin(u/2) \sinh(v/2) \end{align} }[/math]
External links
- Weisstein, Eric W. "Catalan's Surface." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/CatalansSurface.html
- Weiqing Gu, The Library of Surfaces. https://web.archive.org/web/20130317011222/http://www.math.hmc.edu/~gu/curves_and_surfaces/surfaces/catalan.html
References
- ↑ Catalan, E. "Mémoire sur les surfaces dont les rayons de courbures en chaque point, sont égaux et les signes contraires." Comptes rendus de l'Académie des Sciences de Paris 41, 1019–1023, 1855.
- ↑ Ulrich Dierkes, Stefan Hildebrandt, Friedrich Sauvigny, Minimal Surfaces, Volume 1. Springer 2010
- ↑ Gray, A. "Catalan's Minimal Surface." Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, Florida: CRC Press, pp. 692–693, 1997
 |