Physics:Ter-Antonyan function
The Ter-Antonyan function parameterizes the energy spectra of primary cosmic rays in the "knee" region ([math]\displaystyle{ 10^{15}-10^{17} }[/math] eV) by the continuously differentiable function of energy [math]\displaystyle{ E }[/math] taking into account the rate of change of spectral slope. The function is expressed as:
-
[math]\displaystyle{ \frac{dF}{dE} = \Phi E^{-\gamma_1}\left(1+\left(\frac{E}{E_{k}}\right)^{\epsilon}\right)^{\frac{\gamma_1-\gamma_2}{\epsilon}} }[/math],
()
where [math]\displaystyle{ \Phi }[/math] is a scale factor, [math]\displaystyle{ \gamma_1 }[/math] and [math]\displaystyle{ \gamma_2 }[/math] are the asymptotic slopes of the function (or spectral slopes) in a logarithmic scale at [math]\displaystyle{ E\ll E_k }[/math] and [math]\displaystyle{ E\gg E_k }[/math] respectively for a given [math]\displaystyle{ E_k }[/math] energy (the so-called "knee" energy). The rate of change of spectral slopes is set in function (1) by the "sharpness of knee" parameter, [math]\displaystyle{ \epsilon\gt 0 }[/math]. Function (1) was proposed in ANI'98 Workshop (1998) by Samvel Ter-Antonyan[1] for both the interpolation of primary energy spectra in the energy range 1—100 PeV and the search of parametrized solutions of inverse problem to reconstruct primary cosmic ray energy spectra.[1][2] Function (1) is also used for the interpolation of observed Extensive Air Shower spectra in the knee region.[2]
Function (1) can be re-written as:
[math]\displaystyle{ \frac{dF}{dE} = \Phi E^{-\gamma_1}Y(E,\epsilon,\Delta\gamma), }[/math]
where [math]\displaystyle{ \Delta\gamma=\gamma_2-\gamma_1 }[/math] and
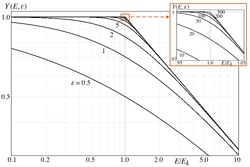
[math]\displaystyle{ Y(E,\epsilon,\Delta\gamma)\equiv\left(1+\left(\frac{E}{E_{k}}\right)^{\epsilon}\right)^{-\frac{\Delta\gamma}{\epsilon}} }[/math]
is the “knee” shaping function describing the change of the spectral slope. Examples of [math]\displaystyle{ Y(E,\epsilon,\Delta\gamma=0.5) }[/math] for [math]\displaystyle{ \epsilon\equiv0.5, 1, 2, \cdots 500 }[/math] are presented above.
The rate of change of spectral slope from [math]\displaystyle{ -\gamma_1 }[/math] to [math]\displaystyle{ -\gamma_2 }[/math] with respect to energy ([math]\displaystyle{ E }[/math]) is derived from (1) as:
[math]\displaystyle{ \frac{df(E)}{dx}=-\gamma_1-\frac{\Delta\gamma}{1+(E_k/E)^\epsilon} }[/math],
where
[math]\displaystyle{ f=\ln\left(\frac{dF}{dE}\right) }[/math],
[math]\displaystyle{ x=\ln(\frac{E}{E_k}) }[/math],
and
[math]\displaystyle{ \left(\frac{df}{dx}\right)_{E=E_k}=-\frac{\gamma_1+\gamma_2}{2} }[/math]
is the sharpness-independent spectral slope at the knee energy.
Function (1) coincides with B. Peters[3] spectra for [math]\displaystyle{ \epsilon=1 }[/math] and asymptotically approaches the broken power law of cosmic ray energy spectra for [math]\displaystyle{ \epsilon\gg1 }[/math]:
[math]\displaystyle{ \left(\frac{dF}{dE}\right)_{\epsilon=\infin}\propto\left(\frac{E}{E_k}\right)^{-\gamma} }[/math],
where
[math]\displaystyle{ \gamma= \begin{cases} \gamma_1, & \text{if } E\lt E_k\\ \gamma_2, & \text{if } E\gt E_k. \end{cases} }[/math]
References
- ↑ 1.0 1.1 S.V. Ter-Antonyan, L.S. Haroyan (2000). About EAS size spectra and primary energy spectra in the knee region.
- ↑ 2.0 2.1 Samvel Ter-Antonyan (2014). "Sharp knee phenomenon of primary cosmic ray energy spectrum". Physical Review D 89 (12): 123003. doi:10.1103/PhysRevD.89.123003. Bibcode: 2014PhRvD..89l3003T.
- ↑ B. Peters (1961). "Primary cosmic radiation and extensive air showers". Nuovo Cimento 22 (4): 800–819. doi:10.1007/BF02783106.
 |