Logarithmic scale
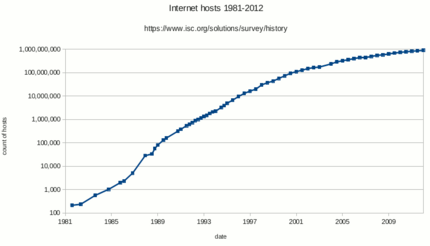
A logarithmic scale (or log scale) is a way of displaying numerical data over a very wide range of values in a compact way. As opposed to a linear number line in which every unit of distance corresponds to adding by the same amount, on a logarithmic scale, every unit of length corresponds to multiplying the previous value by the same amount. Hence, such a scale is nonlinear. In nonlinear scale, the numbers 1, 2, 3, 4, 5, and so on would not be equally spaced. Rather, the numbers 10, 100, 1000, 10000, and 100000 would be equally spaced. Likewise, the numbers 2, 4, 8, 16, 32, and so on, would be equally spaced. Often exponential growth curves are displayed on a log scale, otherwise they would increase too quickly to fit within a small graph.


Common uses
The markings on slide rules are arranged in a log scale for multiplying or dividing numbers by adding or subtracting lengths on the scales.
The following are examples of commonly used logarithmic scales, where a larger quantity results in a higher value:
- Richter magnitude scale and moment magnitude scale (MMS) for strength of earthquakes and movement in the Earth
- Sound level, with units decibel
- Neper for amplitude, field and power quantities
- Frequency level, with units cent, minor second, major second, and octave for the relative pitch of notes in music
- Logit for odds in statistics
- Palermo Technical Impact Hazard Scale
- Logarithmic timeline
- Counting f-stops for ratios of photographic exposure
- The rule of nines used for rating low probabilities
- Entropy in thermodynamics
- Information in information theory
- Particle size distribution curves of soil
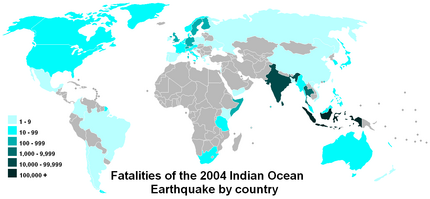
The following are examples of commonly used logarithmic scales, where a larger quantity results in a lower (or negative) value:
- pH for acidity
- Stellar magnitude scale for brightness of stars
- Krumbein scale for particle size in geology
- Absorbance of light by transparent samples
Some of our senses operate in a logarithmic fashion (Weber–Fechner law), which makes logarithmic scales for these input quantities especially appropriate. In particular, our sense of hearing perceives equal ratios of frequencies as equal differences in pitch. In addition, studies of young children in an isolated tribe have shown logarithmic scales to be the most natural display of numbers in some cultures.[1]
Graphic representation
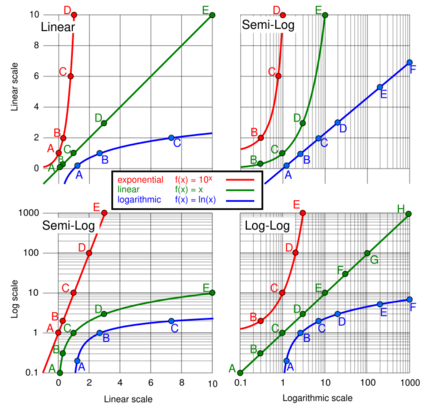
The top left graph is linear in the X and Y axes, and the Y-axis ranges from 0 to 10. A base-10 log scale is used for the Y axis of the bottom left graph, and the Y axis ranges from 0.1 to 1,000.
The top right graph uses a log-10 scale for just the X axis, and the bottom right graph uses a log-10 scale for both the X axis and the Y axis.
Presentation of data on a logarithmic scale can be helpful when the data:
- covers a large range of values, since the use of the logarithms of the values rather than the actual values reduces a wide range to a more manageable size;
- may contain exponential laws or power laws, since these will show up as straight lines.
A slide rule has logarithmic scales, and nomograms often employ logarithmic scales. The geometric mean of two numbers is midway between the numbers. Before the advent of computer graphics, logarithmic graph paper was a commonly used scientific tool.
Log–log plots
If both the vertical and horizontal axes of a plot are scaled logarithmically, the plot is referred to as a log–log plot.
Semi-logarithmic plots
If only the ordinate or abscissa is scaled logarithmically, the plot is referred to as a semi-logarithmic plot.
Extensions
A modified log transform can be defined for negative input (y<0) and to avoid the singularity for zero input (y=0) so as to produce symmetric log plots:[2][3]
for a constant C=1/ln(10).
Logarithmic units
A logarithmic unit is a unit that can be used to express a quantity (physical or mathematical) on a logarithmic scale, that is, as being proportional to the value of a logarithm function applied to the ratio of the quantity and a reference quantity of the same type. The choice of unit generally indicates the type of quantity and the base of the logarithm.
Examples
Examples of logarithmic units include units of information and information entropy (nat, shannon, ban) and of signal level (decibel, bel, neper). Frequency levels or logarithmic frequency quantities have various units are used in electronics (decade, octave) and for music pitch intervals (octave, semitone, cent, etc.). Other logarithmic scale units include the Richter magnitude scale point.
In addition, several industrial measures are logarithmic, such as standard values for resistors, the American wire gauge, the Birmingham gauge used for wire and needles, and so on.
Units of information
Units of level or level difference
Units of frequency level
- decade, decidecade, savart
- octave, tone, semitone, cent
Table of examples
| Unit | Base of logarithm | Underlying quantity | Interpretation |
|---|---|---|---|
| bit | 2 | number of possible messages | quantity of information |
| byte | 28 = 256 | number of possible messages | quantity of information |
| decibel | 10(1/10) ≈ 1.259 | any power quantity (sound power, for example) | sound power level (for example) |
| decibel | 10(1/20) ≈ 1.122 | any root-power quantity (sound pressure, for example) | sound pressure level (for example) |
| semitone | 2(1/12) ≈ 1.059 | frequency of sound | pitch interval |
The two definitions of a decibel are equivalent, because a ratio of power quantities is equal to the square of the corresponding ratio of root-power quantities.[citation needed]
See also
- Alexander Graham Bell
- Bode plot
- Geometric mean (arithmetic mean in logscale)
- John Napier
- Level (logarithmic quantity)
- Log–log plot
- Logarithm
- Logarithmic mean
- Log semiring
- Preferred number
- Semi-log plot
Scale
Applications
References
- ↑ "Slide Rule Sense: Amazonian Indigenous Culture Demonstrates Universal Mapping Of Number Onto Space". 2008-05-30. https://www.sciencedaily.com/releases/2008/05/080529141344.htm.
- ↑ Webber, J Beau W (2012-12-21). "A bi-symmetric log transformation for wide-range data". Measurement Science and Technology (IOP Publishing) 24 (2): 027001. doi:10.1088/0957-0233/24/2/027001. ISSN 0957-0233. https://kar.kent.ac.uk/32810/2/2012_Bi-symmetric-log-transformation_v5.pdf.
- ↑ "Symlog Demo". 2021-05-08. https://matplotlib.org/stable/gallery/scales/symlog_demo.html.
Further reading
- "Log or linear? Distinct intuitions of the number scale in Western and Amazonian indigene cultures". Science 320 (5880): 1217–20. 2008. doi:10.1126/science.1156540. PMID 18511690. Bibcode: 2008Sci...320.1217D.
- "Normzahlen – die einstellige Logarithmentafel des Ingenieurs" (in de). Werkstattechnik und Maschinenbau 43 (4): 156. 1953.
- "Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen" (in de). VDI-Zeitschrift 98: 267–274. 1956.
- (in de) Normung nach Normzahlen (1 ed.). Berlin, Germany: Duncker & Humblot Verlag (de). 1962. ISBN 978-3-42801242-8. (135 pages)
- (in de) Logarithmen, Normzahlen, Dezibel, Neper, Phon - natürlich verwandt!. 2007-09-01. http://www.rechenschieber.org/Normzahlen.pdf. Retrieved 2016-12-18.
External links
- "GNU Emacs Calc Manual: Logarithmic Units". https://www.gnu.org/software/emacs/manual/html_node/calc/Logarithmic-Units.html.
- Non-Newtonian calculus website
 |
