Earth:Ductility (Earth science)

Fig. 1.0 – A vertical viewpoint of a rock outcrop that has undergone ductile deformation to create a series of asymmetric folds.

In Earth science, ductility refers to the capacity of a rock to deform to large strains without macroscopic fracturing. Such behavior may occur in unlithified or poorly lithified sediments, in weak materials such as halite or at greater depths in all rock types where higher temperatures promote crystal plasticity and higher confining pressures suppress brittle fracture. In addition, when a material is behaving ductilely, it exhibits a linear stress vs strain relationship past the elastic limit.

Ductile deformation is typically characterized by diffuse deformation (i.e. lacking a discrete fault plane) and on a stress-strain plot is accompanied by steady state sliding at failure, compared to the sharp stress drop observed in experiments during brittle failure.

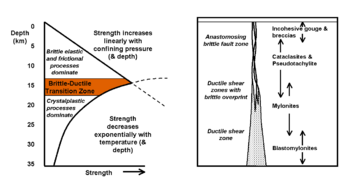
Brittle–Ductile Transition Zone

The brittle–ductile transition zone is characterized by a change in rock failure mode, at an approximate average depth of 10–15 km (~ 6.2–9.3 miles) in continental crust, below which rock becomes less likely to fracture and more likely to deform ductilely. The zone exists because as depth increases confining pressure increases, and brittle strength increases with confining pressure whilst ductile strength decreases with increasing temperature. The transition zone occurs at the point where brittle strength equals ductile strength. In glacial ice this zone is at approximately 30 m (100 ft) depth.

Not all materials, however, abide by this transition. It is possible and not rare for material above the transition zone to deform ductilely, and for material below to deform in a brittle manner. The depth of the material does exert an influence on the mode of deformation, but other substances, such as loose soils in the upper crust, malleable rocks, biological debris, and more are just a few examples of that which does not deform in accordance to the transition zone.

Fig. 1.1 – A generalized diagram of the deformation mechanisms and structural formations that dominate at certain depths within the Earth's crust.

The type of dominating deformation process also has a great impact on the types of rocks and structures found at certain depths within the Earth's crust. As evident from Fig. 1.1, different geological formations and rocks are found in accordance to the dominant deformation process. Gouge and Breccia form in the uppermost, brittle regime while Cataclasite and Pseudotachylite form in the lower parts of the brittle regime, edging upon the transition zone. Mylonite forms in the more ductile regime at greater depths while Blastomylonite forms well past the transition zone and well into the ductile regime, even deeper into the crust.

Quantification

Ductility is a material property that can be expressed in a variety of ways. Mathematically, it is commonly expressed as a total quantity of elongation or a total quantity of the change in cross sectional area of a specific rock until macroscopic brittle behavior, such as fracturing, is observed. For accurate measurement, this must be done under several controlled conditions, including but not limited to Pressure, Temperature, Moisture Content, Sample Size, etc., for all can impact the measured ductility. It is important to understand that even the same type of rock or mineral may exhibit different behavior and degrees of ductility due to internal heterogeneities small scale differences between each individual sample. The two quantities are expressed in the form of a ratio or a percent.

% Elongation of a Rock = [math]\displaystyle{ \%\Delta l = \frac{l_f-l_i}{l_i}\times100 }[/math]

Where:

[math]\displaystyle{ l_i }[/math] = Initial Length of Rock

[math]\displaystyle{ l_f }[/math] = Final Length of Rock

% Change in Area of a Rock = [math]\displaystyle{ \%\Delta A = \frac{A_f-A_i}{A_i}\times100 }[/math]

Where:

[math]\displaystyle{ A_i }[/math] = Initial Area

[math]\displaystyle{ A_f }[/math] = Final Area

For each of these methods of quantifying, one must take measurements of both the initial and final dimensions of the rock sample. For Elongation, the measurement is a uni-dimensional initial and final length, the former measured before any Stress is applied and the latter measuring the length of the sample after fracture occurs. For Area, it is strongly preferable to use a rock that has been cut into a cylindrical shape before stress application so that the cross-sectional area of the sample can be taken.

Cross-Sectional Area of a Cylinder = Area of a Circle = [math]\displaystyle{ A = \pi r^2 }[/math]

Using this, the initial and final areas of the sample can be used to quantify the % change in the area of the rock.

Fig. 1.2 – Stress vs Strain Curve displaying both ductile and brittle deformation behavior.

Deformation

Any material is shown to be able to deform ductilely or brittlely, in which the type of deformation is governed by both the external conditions around the rock and the internal conditions sample. External conditions include temperature, confining pressure, presence of fluids, etc. while internal conditions include the arrangement of the crystal lattice, the chemical composition of the rock sample, the grain size of the material, etc.

Ductilely Deformative behavior can be grouped into three categories: Elastic, Viscous, and Crystal-Plastic Deformation.

Elastic Deformation

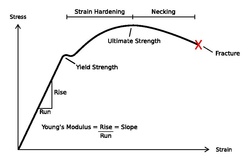
Elastic Deformation is deformation which exhibits a linear stress-strain relationship (quantified by Young's Modulus) and is derived from Hooke's Law of spring forces (see Fig. 1.2). In elastic deformation, objects show no permanent deformation after the stress has been removed from the system and return to their original state.

[math]\displaystyle{ \sigma = E \epsilon }[/math]

Where:

[math]\displaystyle{ \sigma }[/math] = Stress (In Pascals)

[math]\displaystyle{ E }[/math] = Young's Modulus (In Pascals)

[math]\displaystyle{ \epsilon }[/math] = Strain (Unitless)

Viscous Deformation

Viscous Deformation is when rocks behave and deform more like a fluid than a solid. This often occurs under great amounts of pressure and at very high temperatures. In viscous deformation, stress is proportional to the strain rate, and each rock sample has its own material property called its Viscosity. Unlike elastic deformation, viscous deformation is permanent even after the stress has been removed.

[math]\displaystyle{ \sigma = \eta\xi }[/math]

Where:

[math]\displaystyle{ \sigma }[/math] = Stress (In Pascals)

[math]\displaystyle{ \eta }[/math] = Viscosity (In Pascals * Seconds)

[math]\displaystyle{ \xi }[/math] = Strain Rate (In 1/Seconds)

Crystal-Plastic Deformation

Crystal-Plastic Deformation occurs at the atomic scale and is governed by its own set of specific mechanisms that deform crystals by the movements of atoms and atomic planes through the crystal lattice. Like viscous deformation, it is also a permanent form of deformation. Mechanisms of crystal-plastic deformation include Pressure solution, Dislocation creep, and Diffusion creep.

Biological materials

In addition to rocks, biological materials such as wood, lumber, bone, etc. can be assessed for their ductility as well, for many behave in the same manner and possess the same characteristics as abiotic Earth materials. This assessment was done in Hiroshi Yoshihara's experiment, "Plasticity Analysis of the Strain in the Tangential Direction of Solid Wood Subjected to Compression Load in the Longitudinal Direction." The study aimed to analyze the behavioral rheology of 2 wood specimens, the Sitka Spruce and Japanese Birch. In the past, it was shown that solid wood, when subjected to compressional stresses, initially has a linear stress-strain diagram (indicative of elastic deformation) and later, under greater load, demonstrates a non-linear diagram indicative of ductile objects. To analyze the rheology, the stress was restricted to uniaxial compression in the longitudinal direction and the post-linear behavior was analyzed using plasticity theory. Controls included moisture content in the lumber, lack of defects such as knots or grain distortions, temperature at 20 C, relative humidity at 65%, and size of the cut shapes of the wood samples.

Results obtained from the experiment exhibited a linear stress-strain relationship during elastic deformation but also an unexpected non-linear relationship between stress and strain for the lumber after the elastic limit was reached, deviating from the model of plasticity theory. Multiple reasons were suggested as to why this came about. First, since wood is a biological material, it was suggested that under great stress in the experiment, the crushing of cells within the sample could have been a cause for deviation from perfectly plastic behavior. With greater destruction of cellular material, the stress-strain relationship is hypothesized to become more and more nonlinear and non-ideal with greater stress. Additionally, because the samples were inhomogeneous (non-uniform) materials, it was assumed that some bending or distortion may have occurred in the samples that could have deviated the stress from being perfectly uniaxial. This may have also been induced by other factors like irregularities in the cellular density profile and distorted sample cutting.

The conclusions of the research accurately showed that although biological materials can behave like rocks undergoing deformation, there are many other factors and variables that must be considered, making it difficult to standardize the ductility and material properties of a biological substance.

Peak Ductility Demand

Peak Ductility Demand is a quantity used particularly in the fields of architecture, geological engineering, and mechanical engineering. It is defined as the amount of ductile deformation a material must be able to withstand (when exposed to a stress) without brittle fracture or failure. This quantity is particularly useful in the analysis of failure of structures in response to earthquakes and seismic waves.

It has been shown that earthquake aftershocks can increase the peak ductility demand with respect to the mainshocks by up to 10%.