Physics:Tadpole
In quantum field theory, a tadpole is a one-loop Feynman diagram with one external leg, giving a contribution to a one-point correlation function (i.e., the field's vacuum expectation value). One-loop diagrams with a propagator that connects back to its originating vertex are often also referred as tadpoles. For many massless theories, these graphs vanish in dimensional regularization (by dimensional analysis and the absence of any inherent mass scale in the loop integral).
Tadpole corrections are needed if the corresponding external field has a non-zero vacuum expectation value, such as the Higgs field.[1]
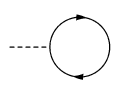
Tadpole diagrams were first used in the 1960s. An early example was published by Abdus Salam in 1961, though he did not take credit for the name.[2] Physicists Sidney Coleman and Sheldon Glashow made an influential use of tadpole diagrams to explain symmetry breaking in the strong interaction in 1964. [3]
In 1985 Coleman stated (perhaps as a joke) that Physical Review’s editors rejected the originally proposed name "spermion".[4][5]
References
- ↑ Evans, Tim. "'Diagramology' Types of Feynman Diagram". https://www.imperial.ac.uk/media/imperial-college/research-centres-and-groups/theoretical-physics/msc/current/qft/handouts/qftdiagramtypes.pdf.
- ↑ Abdus Salam (1961). "Some Speculations on the New Resonances". Reviews of Modern Physics 33 (3): 426–430. doi:10.1103/RevModPhys.33.426. Bibcode: 1961RvMP...33..426S.
- ↑ S. Coleman, S. L. Glashow (1964). "Departures from the Eightfold Way: Theory of Strong Interaction Symmetry Breakdown". Physical Review 134 (3B): B671–B681. doi:10.1103/PhysRev.134.B671. Bibcode: 1964PhRv..134..671C.
- ↑ Coleman, Sidney (2013-02-21). "Notes from Sidney Coleman's Physics 253a". arXiv:1110.5013 [physics.ed-ph].
- ↑ Lancaster, Tom; Blundell, Stephen J. (2014-04-17), "Statistical field theory", Quantum Field Theory for the Gifted Amateur (Oxford University Press): pp. 190, doi:10.1093/acprof:oso/9780199699322.003.0026, ISBN 978-0-19-969932-2, http://dx.doi.org/10.1093/acprof:oso/9780199699322.003.0026, retrieved 2022-04-19

